在平面直角坐标系
中,已知直线l的参数方程为
(t为参数),曲线C的参数方程为
(s为参数).设P为曲线C上的动点,求点P到直线l的距离的最小值.
已知矩阵
,
.
(Ⅰ)求AB;
(Ⅱ)若曲线C 1: =1在矩阵AB对应的变换作用下得到另一曲线C 2 , 求C 2的方程.
对于给定的正整数k,若数列
满足:
对任意正整数
总成立,则称数列{a n}是"
数列".
(Ⅰ)证明:等差数列 是" 数列";
(Ⅱ)若数列 既是"P(2)数列",又是" 数列",证明: 是等差数列.
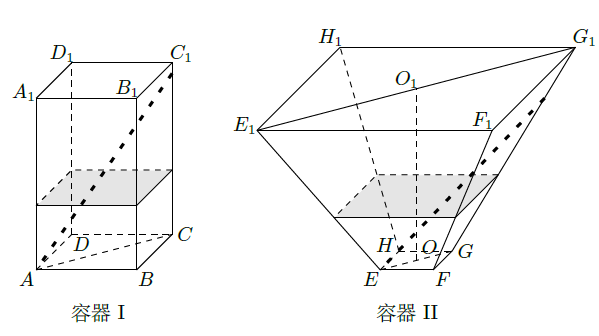
如图,水平放置的正四棱柱形玻璃容器
和正四棱台形玻璃容器
的高均为
,容器
的底面对角线
的长为
cm,容器
的两底面对角线
,
的长分别为
和
.分别在容器
和容器
中注入水,水深均为
.现有一根玻璃棒
,其长度为
.(容器厚度、玻璃棒粗细均忽略不计)
(Ⅰ)将l放在容器 中, 的一端置于点 处,另一端置于侧棱 上,求 没入水中部分的长度;
(Ⅱ)将l放在容器 中, 的一端置于点 处,另一端置于侧棱 上,求 没入水中部分的长度.
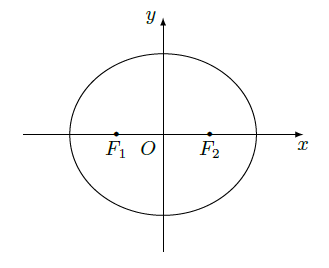
如图,在平面直角坐标系
中,椭圆
的左、右焦点分别为
,
, 离心率为
,两准线之间的距离为
.点P在椭圆E上,且位于第一象限,过点
作直线
的垂线
, 过点
作直线
的垂线
.
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)若直线 , 的交点Q在椭圆E上,求点P的坐标.
已知向量
,
),
.
(Ⅰ)若 ,求x的值;
(Ⅱ)记 ,求 的最大值和最小值以及对应的x的值.
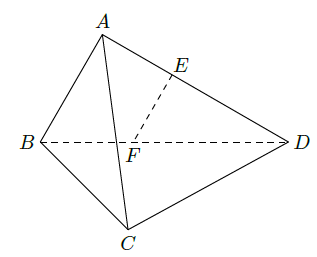
如图,在三棱锥
中,
,
,平面
平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且
.
求证:(Ⅰ)EF∥平面ABC;
(Ⅱ) .
设 是定义在R上且周期为1的函数,在区间[0,1)上, ,其中集合 ,则方程 的解的个数是________.
在平面直角坐标系xOy中,A(﹣12,0),B(0,6),点P在圆O:x 2+y 2=50上.若
,则点P的横坐标的取值范围是________.
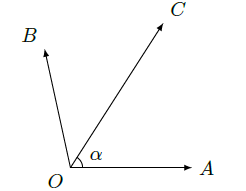
如图,在同一个平面内,向量
,
,
的模分别为1,1,
,
与
的夹角为
,且
,
与
的夹角为
.若
,则
________.
某公司一年购买某种货物600吨,每次购买x吨,运费为6万元/次,一年的总存储费用为4x万元.要使一年的总运费与总存储费用之和最小,则x的值是________.
试题篮
()