高中数学试题

如图，在平面直角坐标系xOy中，椭圆C：的离心率为，短轴长是2．

（1）求a，b的值；
（2）设椭圆C的下顶点为D，过点D作两条互相垂直的直线l₁，l₂，这两条直线与椭圆C的另一个交点分别为M，N．设l₁的斜率为k(k≠0)，△DMN的面积为S，当时，求k的取值范围．

设椭圆C₁:+=1(a>b>0),抛物线C₂:x²+by=b².

(1)若C₂经过C₁的两个焦点,求C₁的离心率;
(2)设A(0,b),Q（3,b）,又M,N为C₁与C₂不在y轴上的两个交点,若△AMN的垂心为B（0,b）,且△QMN的重心在C₂上,求椭圆C₁和抛物线C₂的方程.

在平面直角坐标系xOy中,F是抛物线C:x²=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为.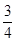
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M的坐标;若不存在,说明理由.
(3)若点M的横坐标为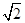,直线l:y=kx+与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当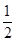≤k≤2时,|AB|²+|DE|²的最小值.

设数列{a_n}的前n项和为S_n.已知a₁＝1，＝a_n＋1－n²－n－，n∈N^*.
(1)求a₂的值；
(2)求数列{a_n}的通项公式；
(3)证明：对一切正整数n，有.

已知数列{b_n}是等差数列，b₁＝1，b₁＋b₂＋…＋b₁₀＝145.
(1)求数列{b_n}的通项公式b_n；
(2)设数列{a_n}的通项a_n＝log_a(其中a＞0且a≠1)．记S_n是数列{a_n}的前n项和，试比较S_n与log_ab_n＋1的大小，并证明你的结论.

已知双曲线-=1(b∈N^*)的左、右两个焦点为F₁、F₂,P是双曲线上的一点,且满足|PF₁||PF₂|=|F₁F₂|²,|PF₂|<4.
(1)求b的值;
(2)抛物线y²=2px(p>0)的焦点与该双曲线的右顶点重合,斜率为1的直线经过右顶点,与该抛物线交于A、B两点,求弦长|AB|.

设抛物线的焦点为，点，线段的中点在抛物线上. 设动直线与抛物线相切于点，且与抛物线的准线相交于点，以为直径的圆记为圆．
（1）求的值；
（2）证明：圆与轴必有公共点；
（3）在坐标平面上是否存在定点，使得圆恒过点？若存在，求出的坐标；若不存在，说明理由．

已知常数，向量，经过定点以为方向向量的直线与经过定点以为方向向量的直线相交于，其中，
（1）求点的轨迹的方程；（2）若，过的直线交曲线于两点，求的取值范围。

定义在上的函数，如果满足：对任意，存在常数，都有 成立，则称是上的有界函数，其中称为函数的一个上界．已知函数，．
（1）若函数为奇函数，求实数的值；
（2）在（1）的条件下，求函数在区间上的所有上界构成的集合；
（3）若函数在上是以3为上界的有界函数，求实数的取值范围．

已知点在椭圆:上，以为圆心的圆与轴相切于椭圆的右焦点，且，其中为坐标原点.
（1）求椭圆的方程；
（2）已知点，设是椭圆上的一点，过、两点的直线交轴于点,若, 求直线的方程;
（3）作直线与椭圆:交于不同的两点,,其中点的坐标为,若点是线段垂直平分线上一点,且满足,求实数的值.

已知数列{a_n}中，a₁＝2，n∈N^*，a_n＞0，数列{a_n}的前n项和为S_n，且满足a_n＋1＝.
(1)求{S_n}的通项公式；
(2)设{b_k}是{S_n}中的按从小到大顺序组成的整数数列．
①求b₃；
②存在N(N∈N^*)，当n≤N时，使得在{S_n}中，数列{b_k}有且只有20项，求N的范围．

已知函数f(x)＝在区间[－1，1]上是增函数．
(1)求实数a的值组成的集合A；
(2)设x₁、x₂是关于x的方程f(x)＝的两个相异实根，若对任意a∈A及t∈[－1，1]，不等式m²＋tm＋1≥|x₁－x₂|恒成立，求实数m的取值范围．

某种产品按下列三种方案两次提价．方案甲：第一次提价p%，第二次提价q%；方案乙：第一次提价q%，第二次提价p%；方案丙：第一次提价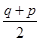%，第二次提价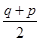%.其中p>q>0，上述三种方案中提价最多的是________．

已知函数．
（1）若在上存在零点，求实数的取值范围；
（2）当时，若对任意的，总存在使成立，求实数的取值范围．

是否存在常数a,b使等式对于一切n∈N*都成立？若存在，求出a,b的值，若不存在，请说明理由。