设抛物线 的焦点为
的焦点为 ,点
,点 ,线段
,线段 的中点在抛物线上.设动直线
的中点在抛物线上.设动直线 与抛物线相切于点
与抛物线相切于点 ,且与抛物线的准线相交于点
,且与抛物线的准线相交于点 ,以
,以 为直径的圆记为圆
为直径的圆记为圆 .
.
(1)求 的值;
的值;
(2)证明:圆 与
与 轴必有公共点;
轴必有公共点;
(3)在坐标平面上是否存在定点 ,使得圆
,使得圆 恒过点
恒过点 ?若存在,求出
?若存在,求出 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
如图,在圆 上任取一点
上任取一点 ,过点
,过点 作
作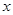 轴的垂线段
轴的垂线段 ,
,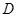 为垂足.设
为垂足.设 为线段
为线段 的中点.
的中点.
(1)当点 在圆
在圆 上运动时,求点
上运动时,求点 的轨迹
的轨迹 的方程;
的方程;
(2)若圆 在点
在点 处的切线与
处的切线与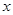 轴交于点
轴交于点 ,试判断直线
,试判断直线 与轨迹
与轨迹 的位置关系.
的位置关系.
已知函数f(x)=(x-a)(x-b)2,a,b是常数.
(1)若a≠b,求证:函数f(x)存在极大值和极小值;
(2)设(1)中f(x)取得极大值、极小值时自变量的值分别为x1,x2,设点A(x1,f(x1)),B(x2,f(x2)).如果直线AB的斜率为- ,求函数f(x)和f′(x)的公共递减区间的长度;
,求函数f(x)和f′(x)的公共递减区间的长度;
(3)若f(x)≥mxf′(x)对于一切x∈R恒成立,求实数m,a,b满足的条件.
已知f1(x)=sin x+cos x,记f2(x)=f1′(x),f3(x)=f2′(x),…,fn(x)=fn-1′(x)(n∈N*,n≥2),则f1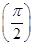 +f2
+f2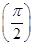 +…+f2 014
+…+f2 014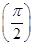 =________.
=________.
已知函数 .
.
(1)当a=1时,求曲线 在点(1,f(1))处的切线方程;
在点(1,f(1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e]上的最小值为-2,求a的值;
(3)若对任意 ,且
,且 恒成立,求a的取值范围.
恒成立,求a的取值范围.
如图,椭圆 上的点M与椭圆右焦点
上的点M与椭圆右焦点 的连线
的连线 与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
(1)求椭圆的离心率;
(2)F1是椭圆的左焦点,C是椭圆上的任一点,证明: ;
;
(3)过 且与AB垂直的直线交椭圆于P、Q,若
且与AB垂直的直线交椭圆于P、Q,若 的面积是20
的面积是20 ,求此时椭圆的方程.
,求此时椭圆的方程.
已知 ,
, ,
, ,其中
,其中 。
。
(1)若 与
与 的图像在交点(2,
的图像在交点(2, )处的切线互相垂直,
)处的切线互相垂直,
求 的值;
的值;
(2)若 是函数
是函数 的一个极值点,
的一个极值点, 和1是
和1是 的两个零点,
的两个零点,
且 ∈(
∈(
 ,求
,求 ;
;
(3)当 时,若
时,若 ,
, 是
是 的两个极值点,当|
的两个极值点,当| -
- |>1时,
|>1时,
求证:| -
- |
|
设,
.
(Ⅰ)求的单调区间和最小值;
(Ⅱ)讨论与
的大小关系;
(Ⅲ)求的取值范围,使得
对任意
成立.
在平面直角坐标系中,直线l:
交
轴于点
,设
是
上一点,
是线段
的垂直平分线上一点,且满足
.
(1)当点在
上运动时,求点
的轨迹
的方程;
(2)已知,设
是
上动点,求
的最小值,并给出此时点
的坐标;
(3)过点且不平行与
轴的直线
与轨迹
有且只有两个不同的交点,求直线
的斜率
的取值范围.
如图,椭圆的中心为原点,离心率
,一条准线的方程为

(Ⅰ)求该椭圆的标准方程.
(Ⅱ)设动点P满足,其中
是椭圆上的点.直线
与
的斜率之积为-0.5.问:是否存在两个定点
,使得
为定值.若存在,求
的坐标;若不存在,说明理由.
试题篮
()