将3k(k为正整数)个石子分成五堆。如果通过每次从其中3堆中各取走一个石子,而最后取完,则称这样的分法是“和谐的”。试给出和谐分法的充分必要条件,并加以证明。
设l,m,n均为直线,其中m,n在平面 内,“l
内,“l
 ”是“l
”是“l m且l
m且l n”的
n”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
函数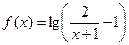 的定义域为集合
的定义域为集合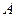 ,函数
,函数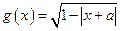 的定义域为集合
的定义域为集合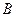 . (1)判定函数
. (1)判定函数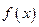 的奇偶性,并说明理由.
的奇偶性,并说明理由.
(2)问: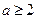 是
是 的什么条件(充分非必要条件 、必要非充分条件、充要条件、既非充分也非必要条件)? 并证明你的结论.
的什么条件(充分非必要条件 、必要非充分条件、充要条件、既非充分也非必要条件)? 并证明你的结论.
条件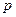 :
: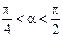 ,条件
,条件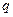 :
: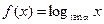 在
在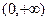 内是增函数,则
内是增函数,则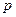 是
是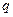 的
的
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
在 中,“
中,“ ”是“
”是“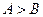 ”的
”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
试题篮
()