某工厂为了对新研发的一种产品进行合理定价,交该产品按事先拟定的价格进行试销,得到如下数据:
单价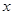 (元) (元) |
4 |
5 |
6 |
7 |
8 |
9 |
销量 (件) (件) |
90 |
84 |
83 |
80 |
75 |
68 |
由表中数据,求得线性回归方程为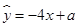 ,若在这些样本点中任取一点,则它在回归直线左下方的概率为
,若在这些样本点中任取一点,则它在回归直线左下方的概率为
A.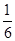 B.
B.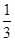 C.
C. D.
D.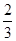
设有一个直线回归方程为 ,则变量
,则变量 增加一个单位时 ( )
增加一个单位时 ( )
A. 平均增加1.5个单位 平均增加1.5个单位 |
B. 平均增加2个单位 平均增加2个单位 |
C. 平均减少1.5个单位 平均减少1.5个单位 |
D. 平均减少2个单位 平均减少2个单位 |
以下命题中:①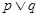 为假命题,则
为假命题,则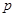 与
与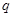 均为假命题
均为假命题
②对具有线性相关的变量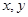 有一组观测数据
有一组观测数据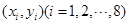 ,其回归直线方程是
,其回归直线方程是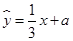 ,且
,且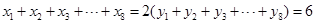 ,则实数
,则实数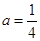
③对于分类变量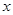 与
与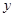 它们的随机变量
它们的随机变量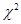 的观测值
的观测值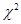 来说
来说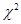 越小.“
越小.“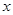 与
与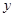 有关联”的把握程度越大
有关联”的把握程度越大
④已知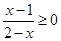 ,则函数
,则函数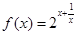 的最小值为16. 其中真命题的个数为 ( )
的最小值为16. 其中真命题的个数为 ( )
| A.0 | B.1 | C.2 | D.3 |
某小卖部销售一品牌饮料的零售价x(元/评)与销售量y(瓶)的关系统计如下:
| 零售价x(元/瓶) |
3.0 |
3.2 |
3.4 |
3.6 |
3.8 |
4.0 |
| 销量y(瓶) |
50 |
44 |
43 |
40 |
35 |
28 |
已知的关系符合线性回归方程 ,其中
,其中 .当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
.当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
A.20 B.22 C.24 D.26
下列说法中正确的是( )
A.若分类变量 和 和 的随机变量 的随机变量 的观测值 的观测值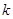 越大,则“ 越大,则“ 与 与 相关”的可信程度越小 相关”的可信程度越小 |
B.对于自变量 和因变量 和因变量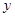 ,当 ,当 取值一定时, 取值一定时,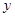 的取值具有一定的随机性, 的取值具有一定的随机性, , ,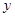 间的这种非确定关系叫做函数关系 间的这种非确定关系叫做函数关系 |
C.相关系数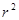 越接近1,表明两个随机变量线性相关性越弱 越接近1,表明两个随机变量线性相关性越弱 |
D.若分类变量 与 与 的随机变量 的随机变量 的观测值 的观测值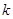 越小,则两个分类变量有关系的把握性越小 越小,则两个分类变量有关系的把握性越小 |
下表是某厂1~4月份用水量(单位:百吨)的一组数据:
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是=-0.7x+a,则a等于( )
| A.10.5 | B.5.15 | C.5.2 | D.5.25 |
从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
| 身高x(cm) |
160 |
165 |
170 |
175 |
180 |
| 体重y(kg) |
63 |
66 |
70 |
72 |
74 |
根据上表可得回归直线方程 ,据此模型预报身高为172cm的高三男生的体重为 ( )
,据此模型预报身高为172cm的高三男生的体重为 ( )
A.70.09kg B.70.12kg C.70.55kg D.71.05kg
通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的2×2列联表:
| |
男 |
女 |
总计 |
| 走天桥 |
40 |
20 |
60 |
| 走斑马线 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
由χ2= 算得,
算得,
χ2=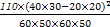 ≈7.8.
≈7.8.
以下结论正确的是( )
(A)有99%以上的把握认为“选择过马路的方式与性别有关”
(B)有99%以上的把握认为“选择过马路的方式与性别无关”
(C)在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”
(D)在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关”
某著名纺织集团为了减轻生产成本继续走高的压力,计划提高某种产品的价格,为此销售部在10月1日至10月5日连续五天对某个大型批发市场中该产品一天的销售量及其价格进行了调查,其中该产品的价格x(元)与销售量y(万件)之间的数据如下表所示:
| 日期 |
10月1日 |
10月2日 |
10月3日 |
10月4日 |
10月5日 |
| 价格x(元) |
9 |
9.5 |
10 |
10.5 |
11 |
| 销售量 y(万件) |
11 |
10 |
8 |
6 |
5 |
已知销售量y与价格x之间具有线性相关关系,其回归直线方程为: =-3.2x+
=-3.2x+ ,若该集团提高价格后该批发市场的日销售量为7.36万件,则该产品的价格约为( )
,若该集团提高价格后该批发市场的日销售量为7.36万件,则该产品的价格约为( )
(A)14.2元 (B)10.8元
(C)14.8元 (D)10.2元
已知一组观测值具有线性相关关系,若对于 =
= x+
x+ ,求得
,求得 =0.51,
=0.51, =61.75,
=61.75, =38.14,则线性回归方程为( )
=38.14,则线性回归方程为( )
A. =0.51x+6.65 =0.51x+6.65 |
B. =6.65x+0.51 =6.65x+0.51 |
C. =0.51x+42.30 =0.51x+42.30 |
D. =42.30x+0.51 =42.30x+0.51 |
变量X与Y相对应的一组数据为(10,1),(11.3,2),
(11.8,3),(12.5,4),(13,5),变量U与V相对应的一组数据为(10,5),(11.3,4),
(11.8,3),(12.5,2),(13,1).r1表示变量Y与X之间的线性相关系数,r2表示变量V与U之间的线性相关系数,则( )
| A.r2<r1<0 | B.0<r2<r1 |
| C.r2<0<r1 | D.r2=r1 |
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程 =3-5x,变量x增加一个单位时,y平均增加5个单位;
=3-5x,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程 =
=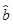 x+
x+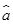 必过(
必过( ,
, );
);
④在一个2×2列联表中,由计算得K2=13.079,则有99%的把握确认这两个变量间有关系.
其中错误的个数是( )
本题可以参考独立性检验临界值表:
| P(K2≥k) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
A.0 B.1 C.2 D.3
观测两个相关变量,得到如下数据:
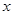 |
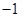 |
 |
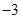 |
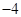 |
 |
5 |
4 |
3 |
2 |
1 |
 |
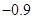 |
 |
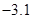 |
 |
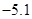 |
5 |
4.1 |
2.9 |
2.1 |
0.9 |
则两变量之间的线性回归方程为( )
A. B.
B. C.
C.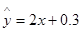 D.
D.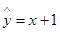
四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
①y与x负相关且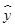 =2.347x-6.423;
=2.347x-6.423;
②y与x负相关且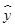 =-3.476x+5.648;
=-3.476x+5.648;
③y与x正相关且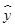 =5.437x+8.493;
=5.437x+8.493;
④y与x正相关且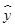 =-4.326x-4.578.
=-4.326x-4.578.
其中一定不正确的结论的序号是( )
| A.①② | B.②③ |
| C.③④ | D.①④ |
四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
①y与x负相关且 =2.347x-6.423;
=2.347x-6.423;
②y与x负相关且 =-3.476x+5.648;
=-3.476x+5.648;
③y与x正相关且 =5.437x+8.493;
=5.437x+8.493;
④y与x正相关且 =-4.326x-4.578.
=-4.326x-4.578.
其中一定不正确的结论的序号是( ).
| A.①② | B.②③ | C.③④ | D.①④ |
试题篮
()