“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
| |
男性 |
女性 |
合计 |
| 反感 |
10 |
|
|
| 不反感 |
|
8 |
|
| 合计 |
|
|
30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路 ”的路人的概率是 .
.
(Ⅰ)请将上面的列表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路 ”与性别是否有关?(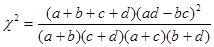
当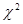 <2.706时,没有充分的证据判定变量性别有关,当
<2.706时,没有充分的证据判定变量性别有关,当
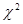 >2.706时,有90%的把握判定变量性别有关,当
>2.706时,有90%的把握判定变量性别有关,当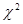 >3.841时,有95%的把握判定变量性别有关,当
>3.841时,有95%的把握判定变量性别有关,当
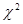 >6.635时,有99%的把握判定变量性别有关)
>6.635时,有99%的把握判定变量性别有关)
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.
(1)请将上面的列联表补充完整;
(2)是否在犯错误的概率不超过0.5%的前提下认为喜爱打篮球与性别有关?说明你的理由.下面的临界值表供参考:
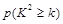 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005] |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: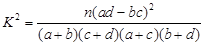 ,其中
,其中 )
)
在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520个女性中6人患色盲,
(1)根据以上的数据建立一个2×2的列联表;
(2)若认为“性别与患色盲有关系”,则出错的概率会是多少
(本题可以参考两个分类变量x和y有关系的可信度表:)
2012年元旦、春节前夕,各个物流公司都出现了爆仓现象,直接原因就是网上疯狂的购物.某商家针对人们在网上购物的态度在某城市进行了一次调查,共调查了124人,其中女性70人,男性54人.女性中有43人对网上购物持赞成态度,另外27人持反对态度;男性中有21人赞成网上购物,另外33人持反对态度.
(Ⅰ) 估计该地区对网上购物持赞成态度的比例;
(Ⅱ) 有多大的把握认为该地区对网上购物持赞成态度与性别有关;
附:表1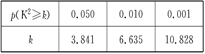
K2=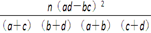
为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:
药物效果试验列联表
| |
患病 |
未患病 |
总计 |
| 没服用药 |
20 |
30 |
50 |
| 服用药 |
x |
y |
50 |
| 总计 |
M |
N |
100 |
设从没服用药的动物中任取两只,未患病数为X;从服用药物的动物中任取两只,未患病数为Y,工作人员曾计算过P(X=0)=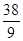 P(Y=0).
P(Y=0).
(1)求出列联表中数据x,y,M,N的值;
(2)能够有多大的把握认为药物有效?
(3)现在从该100头动物中,采用随机抽样方法每次抽取1头,抽后返回,抽取5次, 若每次抽取的结果是相互独立的,记被抽取的5头中为服了药还患病的数量为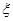 .,求
.,求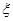 的期望E(
的期望E(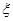 )和方差D(
)和方差D(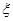 ).
).
参考公式: (其中
(其中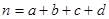 )
)
| P(K2≥k) |
0.25 |
0.15 |
0.10 |
0.05 |
0.010 |
0.005 |
| k |
1.323 |
2.072 |
2.706 |
3.845 |
6.635 |
7.879 |
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
| 单价x(元) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
| 销量y (件 ) |
90 |
84 |
83 |
80 |
75 |
68 |
(I)求销量 与单价
与单价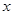 间的回归直线方程;
间的回归直线方程;
(II)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?
在一段时间内,某种商品价格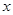 (万元)和需求量
(万元)和需求量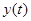 之间的一组数据为:
之间的一组数据为:
价 格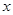 |
1.4 |
1.6 |
1.8 |
2 |
2.2 |
需求量 |
12 |
10 |
7 |
5 |
3 |
(1)进行相关性检验;
(2)如果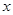 与
与 之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01
之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01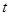 )
)
参考公式及数据: ,
,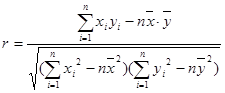 ,
,
相关性检验的临界值表:
| n-2 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 小概率0.01 |
1.000 |
0.990 |
0.959 |
0.917 |
0.874 |
0.834 |
0.798 |
0.765 |
0.735 |
0.708 |
某中学共2200名学生中有男生1200名,按男女性别用分层抽样抽出110名学生,询问是否爱好某项运动。已知男生中有40名爱好该项运动,女生中有30名不爱好该项运动。
(1)如下的列联表:
| |
男 |
女 |
总计 |
| 爱好 |
40 |
|
|
| 不爱好 |
|
30 |
|
| 总计 |
|
|
|
(2)通过计算说明,是否有99%以上的把握认为“爱好该项运动与性别有关”? 参考信息如下:
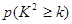 |
0.050 |
0.010 |
0.001 |
| k |
3.841 |
6.635 |
10.828 |
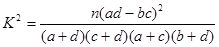
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100棵种子中的发芽数,得到如下资料:
| 日期 |
12月1日 |
12月2日 |
12月3日 |
12月4日 |
12月5日 |
| 温差x(℃) |
10 |
11 |
13 |
12 |
8 |
| 发芽y(颗) |
23 |
25 |
30 |
26 |
16 |
该农科所确定的研究方案是:先从这5组数据中选取3组数据求线性回归方程,剩下的2组数据用于回归方程检验.
回归直线方程参考公式:
 ,
, 

(1)请根据12月2日至12月4日的数据,求出y关于x的线性回归方程 ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则
认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(3)请预测温差为14℃的发芽数。
某种产品的广告费用支出 (百万)与销售额
(百万)与销售额 (百万)之间有如下的对应数据:
(百万)之间有如下的对应数据:
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为10(百万)时,销售收入 的值.
的值.
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:
性别与看营养说明列联表 单位: 名
| |
男 |
女 |
总计 |
| 看营养说明 |
50 |
 |
80 |
| 不看营养说明 |
 |
20 |
30 |
| 总计 |
60 |
50 |
 |
(1)根据以上表格,写出 的值.
的值.
(2)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
某校为了解高二学生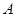 、
、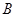 两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试
两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试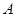 、
、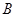 两个学科的合格人数与不合格人数,得到以下2
两个学科的合格人数与不合格人数,得到以下2 2列联表:
2列联表:
| |
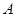 学科合格人数 学科合格人数 |
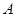 学科不合格人数 学科不合格人数 |
合计 |
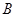 学科合格人数 学科合格人数 |
40 |
20 |
60 |
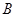 学科不合格人数 学科不合格人数 |
20 |
30 |
50 |
| 合计 |
60 |
50 |
110 |
(1)据此表格资料,你认为有多大把握认为“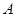 学科合格”与“
学科合格”与“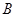 学科合格”有关;
学科合格”有关;
(2)从“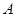 学科合格”的学生中任意抽取2人,记被抽取的2名学生中“
学科合格”的学生中任意抽取2人,记被抽取的2名学生中“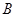 学科合格”的人数为
学科合格”的人数为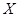 ,求
,求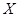 的数学期望.
的数学期望.
附公式与表: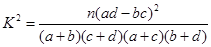
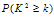 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
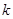 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
某校的研究性学习小组为了研究高中学生的身体发育状况,在该校随机抽出120名17至18周岁的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人数各占一半
(1)根据以上数据建立一个 列联表:
| |
偏重 |
不偏重 |
合计 |
| 偏高 |
|
|
|
| 不偏高 |
|
|
|
| 合计 |
|
|
|
(2)请问该校17至18周岁的男生身高与体重是否有关?
第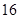 届亚运会于
届亚运会于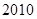 年
年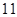 月
月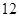 日至
日至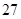 日在中国广州进行,为了做好接待工作,组委会招募了
日在中国广州进行,为了做好接待工作,组委会招募了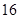 名男志愿者和
名男志愿者和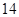 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有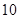 人和
人和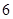 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下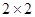 列联表:
列联表:
| |
喜爱运动 |
不喜爱运动 |
总计 |
| 男 |
10 |
|
16 |
| 女 |
6 |
|
14 |
| 总计 |
|
|
30 |
(2)能否在犯错误的概率不超过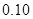 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志愿者中(其中恰有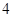 人会外语),抽取
人会外语),抽取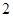 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中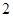 人都能胜任翻译工作的概率是多少?
人都能胜任翻译工作的概率是多少?
附:K2=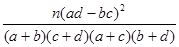
| P(K2≥k) |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
| k |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
试题篮
()