某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
| 商店名称 |
A |
B |
C |
D |
E E |
| 销售额x(千万元) |
3 |
5 |
6 |
7 |
9 9 |
| 利润额y(千万元) |
2 |
3 |
3 |
4 |
5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性。
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.
衡阳市八中对参加“社会实践活动”的全体志愿者进行学分考核,因该批志愿者表现良好,学校决定考核只有合格和优秀两个等次.若某志愿者考核为合格,授予1个学分;考核为优秀,授予2个学分,假设该校志愿者甲、乙、丙考核为优秀的概率分别为 、
、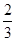 、
、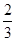 ,他们考核所得的等次相互独立.
,他们考核所得的等次相互独立.
(1)求在这次考核中,志愿者甲、乙、丙三人中至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名志愿者所得学分之和为随机变量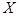 ,求随机变量
,求随机变量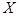 的分布列及数学期望.
的分布列及数学期望.
设三组实验数据(x1,y1),(x2,y2),(x3,y3)的回归直线方程是: =
= x+
x+ ,使代数式[y1-(
,使代数式[y1-( x1+
x1+ )]2+[y2-(
)]2+[y2-( x2+
x2+ )]2+[y3-(
)]2+[y3-( x3+
x3+ )]2的值最小时,
)]2的值最小时, =
= -
-
 ,
, =
=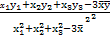 (
( ,
, 分别是这三组数据的横、纵坐标的平均数),
分别是这三组数据的横、纵坐标的平均数),
若有7组数据列表如下:
| x |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
4 |
6 |
5 |
6.2 |
8 |
7.1 |
8.6 |
(1)求上表中前3组数据的回归直线方程.
(2)若|yi-( xi+
xi+ )|≤0.2,即称(xi,yi)为(1)中回归直线的拟合“好点”,求后4组数据中拟合“好点”的概率.
)|≤0.2,即称(xi,yi)为(1)中回归直线的拟合“好点”,求后4组数据中拟合“好点”的概率.
从某居民区随机抽取10个家庭,获得第个家庭的月收入
(单位:千元)与月储蓄
(单位:千元)的数据资料,算得
.(1)求家庭的月储蓄
对月收入
的线性回归方程
;
(2)判断变量与
之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程中,
,其中
为样本平均值,线性回归方程也可写为
.
为治疗一种慢性病,某医药研究所研究出一种新型药物,病人按规定的剂量服用该药物后,测得每毫升血液中含药量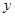 (毫克)与时间
(毫克)与时间 (小时)满足:前1小时内成正比例递增,1小时后按指数型函数
(小时)满足:前1小时内成正比例递增,1小时后按指数型函数 (
( 为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
(1)求函数 的解析式;
的解析式;
(2)已知每毫升血液中含药量不低于0.5毫克时有治疗效果,低于0.5毫克时无治疗效果.求病人一次服药后的有效治疗时间为多少小时?
为了解高二某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表: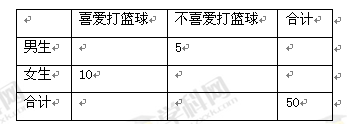
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
下面的临界值表供参考:
(参考公式K2= ,其中n=a+b+c+d)
,其中n=a+b+c+d)
由某种设备的使用年限 (年)与所支出的维修费
(年)与所支出的维修费 (万元)的数据资料,算得
(万元)的数据资料,算得 ,
, ,
, ,
,  .
.
(Ⅰ)求所支出的维修费 对使用年限
对使用年限 的线性回归方程
的线性回归方程 ;
;
(Ⅱ)判断变量 与
与 之间是正相关还是负相关;
之间是正相关还是负相关;
(Ⅲ)估计使用年限为8年时,支出的维修费约是多少.
附:在线性回归方程 中,
中, ,
, ,其中
,其中 ,
, 为
为
样本平均值,线性回归方程也可写为 .
.
.以下是粤西地区某县搜集到的新房屋的销售价格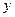 和
和 房屋的面积
房屋的面积 的数据:
的数据: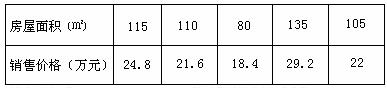
(1)画出数据散点图;
(2)由散点图判断新房屋销售价格y和房屋面积x是否具有线性相关关系?若有,求线性回 归方程。(保留四位小数)
归方程。(保留四位小数)
(3)根据房屋面积预报销售价格的回归方程,预报房屋面积为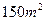 时的销售价格。
时的销售价格。
参考公式: 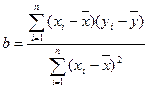 ,
,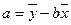
参考数据: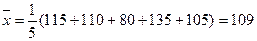 ,
,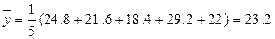
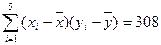 ,
,
(满分12分)假设关于某设备的使用年限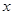 和所支出的维修费用
和所支出的维修费用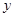 (万元)有如下的统计资料:
(万元)有如下的统计资料:
使用年限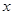 |
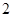 |
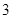 |
 |
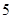 |
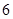 |
维修费用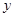 |
 |
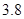 |
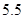 |
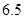 |
 |
若由资料知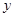 对
对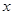 呈线性相关关系。
呈线性相关关系。
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程 的回归系数
的回归系数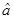 ,
,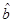 .
.
(3)估计使用年限为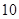 年时,维修费用是多少?
年时,维修费用是多少?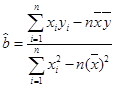 ,
,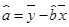
(本小题满分12分)某地区2007年至2013年农村居民家庭纯收入 (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
| 年份 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
年份代号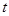 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
人均纯收入 |
2.9 |
3.3 |
3.6 |
4.4 |
4.8 |
5.2 |
5.9 |
(Ⅰ)求 关于
关于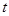 的线性回归方程;(已知b=0.5)
的线性回归方程;(已知b=0.5)
(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
为了预防甲型H1N1流感,某学校对教室用药薰消毒法进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与t时间(小时)成正比,药物释放完毕后,y与t之间的函数关系式为 (a为常数)如下图所示,根据图中提供的信息,回答下列问题.
(a为常数)如下图所示,根据图中提供的信息,回答下列问题.
(1)从药物释放开始,求每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始至少需要经过多少小时后,学生才可能回到教室.
(本小题满分12分)
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 |
1月10日 |
2月10日 |
3月10日 |
4月10日 |
5月10日 |
6月10日 |
昼夜温差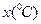 |
10 |
11 |
13 |
12 |
8 |
6 |
就诊人数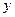 个 个 |
22 |
25 |
29 |
26 |
16 |
12 |
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
⑴求选取的2组数据恰好是相邻两个月的概率;
⑵若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出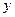 关于
关于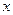 的线性回归方程
的线性回归方程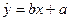 ;
;
⑶若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(本小题满分12分)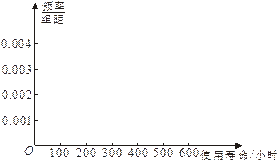
对某电子元件进行寿命追踪调查,情况如下:
| 寿命/小时 |
100~200 |
200~300 |
300~400 |
400~500 |
500~600 |
| 个数 |
20 |
30 |
80 |
40 |
30 |
(1)完成频率分布表;
| 分组 |
频数 |
频率 |
| 100~200 |
|
|
| 200~300 |
|
|
| 300~400 |
|
|
| 400~500 |
|
|
| 500~600 |
|
|
| 合计 |
|
|
(2)画出频率分布直方图和频率分布折线图;
(3)估计电子元件寿命在100~400小时以内的频率;
由某种设备的使用年限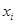 (年)与所支出的维修费
(年)与所支出的维修费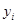 (万元)的数据资料算得如下结果,
(万元)的数据资料算得如下结果, ,
, ,
, ,
,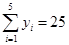 .
.
(1)求所支出的维修费y对使用年限x的线性回归方程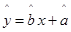 ;
;
(2)①判断变量x与y之间是正相关还是负相关;
②当使用年限为8年时,试估计支出的维修费是多少.
(附:在线性回归方程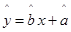 中,)
中,)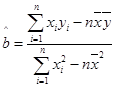 ,
, ,其中
,其中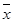 ,
,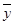 为样本平均值.)
为样本平均值.)
试题篮
()