下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量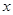 (吨)与相应的生产能耗
(吨)与相应的生产能耗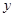 (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
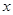 |
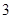 |
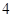 |
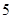 |
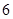 |
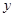 |
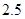 |
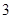 |
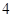 |
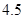 |
(1)请根据上表提供的数据,求出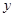 关于
关于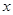 的线性回归方程
的线性回归方程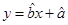 ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
某个体服装店经营某种服装,在某周内获纯利y(元)与该周每天销售这种服装件数x之间的一组数据关系如下表:
已知: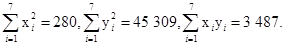
(1)求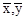 ;
;
(2)画出散点图;你从散点图中发现该种服装的销售件数x与纯利润y(元)之间有什么统计规律吗?
(3)求纯利y与每天销售件数x之间的线性回归方程;
(4)若该周内某天销售服装20件,估计可获纯利多少元?
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验如下:
零件的个数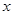 (个) (个) |
2 |
3 |
4 |
5 |
加工的时间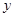 (小时) (小时) |
2.5 |
3 |
4 |
4.5 |
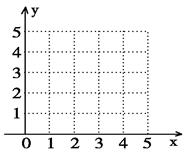
(1)在给定坐标系中画出表中数据的散点图;
(2)求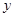 关于
关于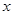 的线性回归方程
的线性回归方程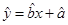 ;
;
(3)试预测加工10个零件需要多少时间?
(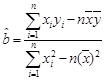 ,
,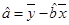 )
)
假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:若由资料知y对x呈线性相关关系.
(1)请根据最小二乘法求出线性回归方程.
(2)估计使用年限为10年时,维修费用是多少?
为了调查胃病是否与生活规律有关,调查某地540名40岁以上的人得结果如下:
| |
患胃病 |
未患胃病 |
合计 |
| 生活不规律 |
60 |
260 |
320 |
| 生活有规律 |
20 |
200 |
220 |
| 合计 |
80 |
460 |
540 |
根据以上数据回答40岁以上的人患胃病与生活规律有关吗?
某商店统计了最近6个月某商品的进价x(元)与售价y(元)的对应数据如下表:
| x |
3 |
5 |
2 |
7 |
8 |
11 |
| y |
4 |
6 |
3 |
9 |
12 |
14 |
则回归直线方程是_______________.
注:线性回归直线方程系数公式: 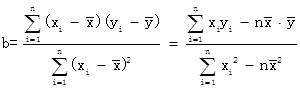 ,a=y-bx
,a=y-bx
(本小题满分13分)
某种产品的广告费支出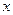 与销售额
与销售额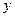 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
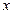 |
2 |
4 |
5 |
6 |
8 |
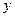 |
30 |
40 |
60 |
50 |
70 |
(Ⅰ)求回归直线方程;
(Ⅱ)试预测广告费支出为10万元时,销售额多大?
(Ⅲ)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的
绝对值不超过5的概率。
(参考数据: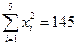
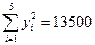
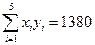 ,
,
参考公式:回归直线方程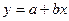 ,其中
,其中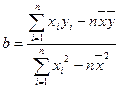 )
)
在电阻碳含量对于电阻的效应研究中,得到如下表所示的数据:
| 含碳量 (x/%) |
0.10 |
0.30 |
0.40 |
0.55 |
0.70 |
0.80 |
0.95 |
| 20 ℃时电阻 (y/Ω) |
15 |
18 |
19 |
21 |
22.6 |
23.8 |
26 |
(1)求出y与x的相关系数并判断相关性;
(2)求出电阻y关于含碳量x之间的回归直线方程.
某地10户家庭的年收入和年饮食支出的统计资料如下表:
| 年收入 x(万元) |
2 |
4 |
4 |
6 |
6 |
6 |
7 |
7 |
8 |
10 |
| 年饮食支出 y(万元) |
0.9 |
1.4 |
1.6 |
2.0 |
2.1 |
1.9 |
1.8 |
2.1 |
2.2 |
2.3 |
(1)根据表中数据,确定家庭的年收入和年饮食支出之间是否具有相关关系;若具有相关关系求出y与x的回归直线方程;
(2)如果某家庭年收入为9万元,预测其年饮食支出.
测得某国家10对父子身高(单位:英寸)如下:
| 父亲身高(x) |
60 |
62 |
64 |
65 |
66 |
67 |
68 |
70 |
72 |
74 |
| 儿子身高(y) |
63.6 |
65.2 |
66 |
65.5 |
66.9 |
67.1 |
67.4 |
68.3 |
70.1 |
70 |
(1)对变量y与x进行相关性检验;
(2)如果y与x之间具有线性相关关系,求回归直线方程;
(3)如果父亲的身高为73英寸,估计儿子的身高.
(本小题满分12分)
某研究机构对高三学生的记忆力 和判断力
和判断力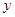 进行统计分析,得下表数据:
进行统计分析,得下表数据:
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
(1)画出散点图并指出 与
与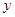 之间是正相关还是负相关 ;
之间是正相关还是负相关 ;
(2)请根据上表提供的数据,用最小二乘法求出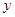 关于
关于 的线性回归方程
的线性回归方程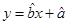 ;
;
其中(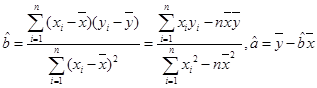 )
)
(3)记忆力为14的同学的判断力约为多少?
(本小题满分12分)某地区2007年至2013年农村居民家庭纯收入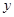 (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
| 年份 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
年份代号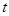 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
人均纯收入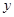 |
2.9 |
3.3 |
3.6 |
4.4 |
4.8 |
5.2 |
5.9 |
(Ⅰ)求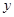 关于
关于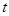 的线性回归方程;(已知b=0.5)
的线性回归方程;(已知b=0.5)
(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
为了对新产品进行合理定价,对该产品进行了试销试验,以观察需求量Y(单位:千件)对于价格x(单位:千元)的反应,得数据如下:
| x/千元 |
50 |
70 |
80 |
40 |
30 |
90 |
95 |
97 |
| y/千件 |
100 |
80 |
60 |
120 |
135 |
55 |
50 |
48 |
(1)若y与x之间具有线性相关关系,求y对x的回归直线方程;
(2)若成本x=y+500,试求:
①在盈亏平衡条件下(利润为零)的价格;
②在利润为最大的条件下,定价为多少?
(满分12分)假设关于某设备的使用年限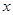 和所支出的维修费用
和所支出的维修费用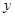 (万元)有如下的统计资料:
(万元)有如下的统计资料:
使用年限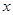 |
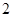 |
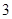 |
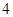 |
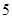 |
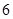 |
维修费用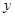 |
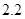 |
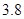 |
 |
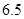 |
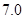 |
若由资料知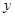 对
对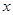 呈线性相关关系。
呈线性相关关系。
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程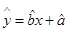 的回归系数
的回归系数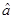 ,
,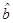 .
.
(3)估计使用年限为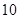 年时,维修费用是多少?
年时,维修费用是多少?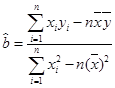 ,
,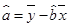
试题篮
()