某商场在销售过程中投入的销售成本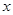 与销售额
与销售额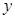 的统计数据如下表:
的统计数据如下表:
| 销售成本x(万元) |
3 |
4 |
6 |
7 |
销售额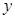 (万元) (万元) |
25 |
34 |
49 |
56 |
根据上表可得,该数据符合线性回归方程: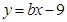 .由此预测销售额为100万元时,投入的销售成本大约为 ;
.由此预测销售额为100万元时,投入的销售成本大约为 ;
下列说法中正确的是 (填序号)
①回归分析就是研究两个相关事件的独立性;
②回归模型都是确定性的函数;
③回归模型都是线性的;
④回归分析的第一步是画散点图或求相关系数 ;
;
⑤回归分析就是通过分析、判断,确定相关变量之间的内在的关系的一种统计方法.
某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据:由资料显示 对
对 呈线性相关关系。
呈线性相关关系。
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
根据上表提供的数据得到回归方程 中的
中的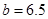 ,预测销售额为115万元时约需万元广告费
,预测销售额为115万元时约需万元广告费
下列叙述中:
①变量间关系有函数关系,还有相关关系;②回归函数即用函数关系近似地描述相关关系;③ ;④线性回归方程一定可以近似地表示所有相关关系.
;④线性回归方程一定可以近似地表示所有相关关系.
其中正确的有
某产品广告费用x与销售额y的统计数据如下表:
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
54 |
根据上表可得回归直线方程 中的
中的 为9.4,据此模型预报广告费用为6万元时销售额为 .
为9.4,据此模型预报广告费用为6万元时销售额为 .
某单位为了了解用电量y度与气温x℃之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
| x |
18 |
13 |
10 |
-1 |
| y |
25 |
34 |
39 |
62 |
由表中数据得线性回归方程y=-2x+a,预测当气温为-4 ℃时,用电量的度数约为 .
下表是某厂1-4月份用水量(单位:100t)的一组数据, 由其散点图可知, 用水量y与月份x之间有较好的线性相关关系,其线性回归方程是_________________.
| 月份x |
1 |
2 |
3 |
4 |
| 用水量y(100t) |
4.4 |
4 |
3 |
2.5 |
某次测量发现一组数据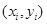 具有较强的相关性,并计算得
具有较强的相关性,并计算得  ,其中数据
,其中数据 ,Y)因书写不清,只记得
,Y)因书写不清,只记得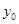 是[0,3]内的任意一个值,则该数据对应的残差的绝对值不大于l的概率为__________.(残差=真实值一预测值)
是[0,3]内的任意一个值,则该数据对应的残差的绝对值不大于l的概率为__________.(残差=真实值一预测值)
已知x,Y之间的数据如下表所示,则Y与x之间的线性回归直线一定过点________.
| x |
1.08 |
1.12 |
1.19 |
1.28 |
| Y |
2.25 |
2.37 |
2.40 |
2.55 |
下表为某公司员工连续加班时间与制造产品的几组数据,根据表中提供的数据,求出y关于 的线性回归方程为
的线性回归方程为 ,则表中t的值为 .
,则表中t的值为 .
 |
3 |
4 |
5 |
6 |
 |
2.5 |
t |
4 |
4.5 |
试题篮
()