【改编题】已知x,y的值如下表所示:
| x |
2 |
3 |
4 |
| y |
5 |
4 |
6 |
如果y与x呈线性相关,则回归方程为 所表示的直线经过的定点为_______.
所表示的直线经过的定点为_______.
一个车间为了规定工作定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下:
由表中数据,求得线性回归方程 ,根据回归方程,
,根据回归方程,
预测加工70个零件所花费的时间为 分钟.
某单位为了了解用电量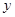 (度)与当天平均气温
(度)与当天平均气温 (°C)之间的关系,随机统计了某4天的当天平均气温与用电量(如右表)。由数据运用最小二乘法得线性回归方程
(°C)之间的关系,随机统计了某4天的当天平均气温与用电量(如右表)。由数据运用最小二乘法得线性回归方程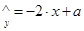 ,则
,则 __________.
__________.
平均气温 (°C) (°C) |
18 |
13 |
10 |
-1 |
用电量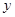 (度) (度) |
25 |
35 |
37 |
63 |
下列关于回归分析的说法正确的是 (填上所有正确说法的序号)
①相关系数 越小,两个变量的相关程度越弱;②残差平方和越大的模型,拟合效果越好;③用相关指数
越小,两个变量的相关程度越弱;②残差平方和越大的模型,拟合效果越好;③用相关指数 来刻画回归效果时,
来刻画回归效果时, 越小,说明模型的拟合效果越好;④用最小二乘法求回归直线方程,是寻求使
越小,说明模型的拟合效果越好;④用最小二乘法求回归直线方程,是寻求使 取最小值时的
取最小值时的 的值;⑤在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适,这样的带状区域的宽度越窄,模型拟合精度越高.
的值;⑤在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适,这样的带状区域的宽度越窄,模型拟合精度越高.
某产品在某零售摊位的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如下表所示:由上表可得回归直线方程 中的
中的 ,据此模型预测零售价为15元时,每天的销售量为 .
,据此模型预测零售价为15元时,每天的销售量为 .

人们在生活和消费过程中的过量碳排放,是造成全球气候变暖的重要因素之一,所谓“低碳生活”就是指生活作息时所耗用的能量要尽力减少,从而减低二氧化碳的排放量.某单位为了制定节能减排的目标,先调查了用电量 (度)与气温
(度)与气温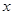 (
(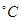 )之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温(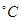 ) ) |
18 |
13 |
10 |
 |
| 用电量(度) |
24 |
34 |
38 |
64 |
由表中数据,得线性回归方程 ,当气温为
,当气温为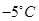 时,预测用电量的度数约为 .
时,预测用电量的度数约为 .
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗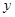 (吨标准煤)的几组对应数据﹒
(吨标准煤)的几组对应数据﹒
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
m |
4 |
4.5 |
根据上表提供的数据,求出y关于x的线性回归方程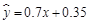 ,那么表中m的值为 .
,那么表中m的值为 .
某批发市场对某件商品(成本为5元/件)进行了6天的试销,得到如下数据:
单价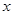 (元) (元) |
8.00 |
8.20 |
8.40 |
8.60 |
8.80 |
9.00 |
销量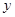 (件) (件) |
90 |
84 |
83 |
80 |
75 |
68 |
经分析发现销量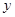 (件)与单价
(件)与单价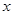 (元)具有线性相关关系,且回归直线方程为
(元)具有线性相关关系,且回归直线方程为 (其中,
(其中,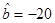 ,
, ),那么今后为了获得最大利润,该商品的的单价应定为 元.
),那么今后为了获得最大利润,该商品的的单价应定为 元.
某企业对自己的拳头产品的销售价格(单位:元)与月销售量(单位:万件)进行调查,其中最近五个月的统计数据如下表所示:
价格 |
9 |
 |
 |
 |
11 |
销售量 |
11 |
 |
8 |
6 |
5 |
由散点图可知,销售量 与价格
与价格 之间有较强的线性相关关系,其线性回归直线方程是:
之间有较强的线性相关关系,其线性回归直线方程是: ,且
,且 ,则
,则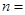 ___
___
某企业对自己的拳头产品的销售价格(单位:元)与月销售量(单位:万件)进行调查,其中最近五个月的统计数据如下表所示:
价格 |
9 |
 |
 |
 |
11 |
销售量 |
11 |
 |
8 |
6 |
5 |
由散点图可知,销售量 与价格
与价格 之间有较强的线性相关关系,其线性回归直线方程是:
之间有较强的线性相关关系,其线性回归直线方程是: ,且
,且 ,则
,则 ___
___
对具有线性相关关系的变量 和
和 ,测得一组数据如下:
,测得一组数据如下:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
若已求得它们的回归方程的斜率为6.5,则这条直线的回归方程为 .
试题篮
()