已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.9,则P(0<ξ<2)=( )
| A.0.2 | B.0.3 | C.0.4 | D.0.6 |
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下图频率分布直方图:

(I)求这500件产品质量指标值的样本平均值和样本方差
(同一组的数据用该组区间的中点值作代表);
(II)由直方图可以认为,这种产品的质量指标服从正态分布
 ,其中
,其中近似为样本平均数
,
 近似为样本方差
近似为样本方差.
(i)利用该正态分布,求;
(ii)某用户从该企业购买了100件这种产品,记表示这100件产品中质量指标值位于区间
的产品件数.利用(i)的结果,求
.
附:
若 则
则 ,
, 。
。
在某市组织的一次数学竞赛中全体参赛学生的成绩近似服从正态分布N(60,100),已知成绩在90分以上(含90分)的学生有13人.
(1)求此次参加竞赛的学生总数共有多少人?
(2)若计划奖励竞赛成绩排在前228名的学生,问受奖学生的分数线是多少?
.某城市从南郊某地乘公共汽车前往北区火车站有两条路线可走,第一条路线穿过
市区,路线较短,但交通拥挤,所需时间(单位为分)服从正态分布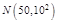 ;第二条
;第二条
路线沿环城公路走,路程较长,但交通阻塞少,所需时间服从正态分布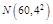 .
.
(1)若只有70分钟可用,问应走哪条路线?
(2)若只有65分钟可用,又应走哪条路线
灯泡厂生产的白炽灯寿命X(单位:h),已知X~N(1 000,302),要使灯泡的平均寿命为1 000 h的概率为99.7%,问灯泡的平均寿命应控制在多少小时以上?
在某次数学考试中,考生的成绩 服从一个正态分布,即
服从一个正态分布,即 ~N(90,100).
~N(90,100).
(1)试求考试成绩 位于区间(70,110)上的概率是多少?
位于区间(70,110)上的概率是多少?
(2)若这次考试共有2 000名考生,试估计考试成绩在(80,100)间的考生大约有多少人?
某市有210名初中学生参加数学竞赛预赛,随机调阅了60名学生的答卷,成绩列表如下:
| 成绩 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 人数分布 |
0 |
0 |
0 |
6 |
15 |
21 |
12 |
3 |
3 |
0 |
(1)求样本的数学平均成绩及标准差;(精确到0.01)
(2)若总体服从正态分布,求此正态曲线的近似方程.
工厂制造的某机械零件尺寸X服从正态分布N(4, ),问在一次正常的试验中,取1 000个零件时,不属于区间(3,5)这个尺寸范围的零件大约有多少个?
),问在一次正常的试验中,取1 000个零件时,不属于区间(3,5)这个尺寸范围的零件大约有多少个?
标准正态分布的概率密度函数是P(x)= ·
· (x∈R).
(x∈R).
(1)求证:P(x)是偶函数;
(2)求P(x)的最大值;
(3)利用指数函数的性质说明P(x)的增减性.
试题篮
()