高中数学合情推理和演绎推理选择题

“∵四边形ABCD是等腰梯形，∴四边形ABCD的对角线相等.”补充以上推理的大前提（ ）

A．正方形都是对角线相等的四边形	B．矩形都是对角线相等的四边形
C．等腰梯形都是对角线相等的四边形	D．矩形都是对边平行且相等的四边形

个连续自然数按规律排列如下：

根据规律，从2011到2013箭头方向依次是（    ）

A．↓→

B．→↑

C．↑→

D．→↓

“所有9的倍数都是3的倍数，某奇数是9的倍数，故该奇数是3的倍数．”上述推
理（  ） 

A．小前提错

B．结论错

C．正确

D．大前提错

按照下列三种化合物的结构式及分子式的规律，写出后一种化合物的分子式是（  ）.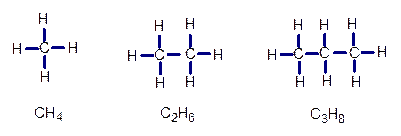

A．C4H9

B．C4H10

C．C4H11

D．C6H12

. 5名志愿者分到3所学校支教，每个学校至少去一名志愿者，则不同的分派方法共有（    ）

A．150种

B．180种

C．200种

D．280种

设，则（  ）

A．

B．

C．

D．

用数学归纳法证明对n为正偶数时某命题成立，若已假设为偶数）时命题为真，则还需要用归纳假设再证                     （  ）

A．时等式成立	B．时等式成立
C．时等式成立	D．时等式成立

定义运算，则符合条件的复数对应的点在（   ）

A．第一象限；

B．第二象限；

C．第三象限；

D．第四象限；

古希腊人常用小石子在沙滩上摆成各种形状来研究数，例如： .   
他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数；类似地，称图2中的1，4，9，16…这样的数成为正方形数.下列数中及时三角形数又是正方形数的是（ ）

A．289

B．1024

C．1225

D．1378

古希腊人常用小石子在沙滩上摆成各种形状来研究数。比如：

他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数；类似的，称图2中的1，4，9，16，…这样的数为正方形数。下列数中既是三角形数又是正方形数的是（    ）.

A．289

B．1024

C．1225

D．1378

从推理形式上看，由特殊到特殊的推理，由部分到整体，个别到一般的推理，由一般到特殊的推理依次是（）

A．归纳推理、演绎推理、类比推理	B．类比推理、归纳推理、演绎推理
C．归纳推理、类比推理、演绎推理	D．演绎推理、归纳推理、类比推理

下面几种推理过程是演绎推理的是

A．两条直线平行，同旁内角互补，如果和是两条平行线的同旁内角，则；

B．由平面三角形的性质，推测空间四面体的性质；

C．某校共有10个班，1班有51人，2班有53人，3班有52人，由此推测各班都超过50人；

D．在数列中，，由此归纳出的通项公式．

下列几种推理是演绎推理的是（    ）

A．在数列中，，由此归纳出的通项公式

B．某高校高三（1）班有55人，（2）班有54人，（3）班有52人，由此得出高三所有班级的人数都超过50人。

C．由平面三角形的性质，推测出空间四面体的性质

D．两条直线平行，同旁内角互补。如果是两条直线的同旁内角，则

．已知①正方形的对角线相等，②矩形的对角线相等，③正方形是矩形。根据“三段论”推理出一个结论，则这个结论是 （   ）

A．正方形的对角线相等

B．矩形的对角线相等

C．正方形是矩形

D．其它

已知数列的前项和，而，通过计算，猜想=（   ）

A．

B．

C．

D．