已知①正方形的对角线相等;②矩形的对角线相等;③正方形是矩形.根据”三段论”推理出一个结论。则这个结论是( )
| A.正方形的对角线相等 | B.矩形的对角线相等 | C.正方形是矩形 | D.其 他 他 |
下面几种推理过程是演绎推理的是( )
A.两条直线平行,同旁内角互补,如果 与 与 是两条平行直线的同旁内角,则 是两条平行直线的同旁内角,则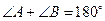 。 。 |
| B.某校高二(1)班有55人,高二(2)班有52人,由此得高二所有班人数超过50人。 |
C. 由平面三角形的性质,推出空间四边形的性质。 由平面三角形的性质,推出空间四边形的性质。 |
D.在数列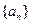 中, 中,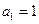 , ,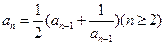 ,通过计算 ,通过计算 , , , , 由此归纳出 由此归纳出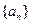 的通项公式。 的通项公式。 |
命题“有理数是无限循环小数,整数是有 理数,所以整数是无限循环小数”是假命题,推理错误的原因是( )
理数,所以整数是无限循环小数”是假命题,推理错误的原因是( )
| A.使用了归纳推理 | B.使用类比推理 |
| C.使用三段论,但大前提错误 | D.使用三段论,但小前提错误 |
一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示. 某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断:① 0点到3点只进水不出水; ②3点到4点不进水只出水; ③4点到6点不进水不出水. 则正确论断的个数是( )
| A.3 | B.2 | C.1 | D. 0 |

下面几种推理是类比推理的是( )
A.两条直线平行,同旁内角互补,如果 和 和 是两条平行直线的 是两条平行直线的 同旁内角,则 同旁内角,则  |
| B.由平面向量的运算性质,推测空间向量的运算性质 |
| C.某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员 |
D.一切偶数都能被2整除, 是偶数,所以 是偶数,所以 能被2整除 能被2整除 |
“因为四边形ABCD是矩形,所四边形ABCD的对角线相等”,补充以上推理的大前提是  ( )
( )
| A.矩形都是四边形; | B.四边形的对角线都相等; |
| C.矩形都是对角线相等的四边形; | D.对角线都相等的四边形是矩形 |
有一段演绎推理是这样的:“因为一次函数 =
= +
+ (
( 在R上是增函数,而
在R上是增函数,而 =
= +
+ 是一次函数,所以
是一次函数,所以 =
= +
+ 在R上是增函数” 的结论显然是错误
在R上是增函数” 的结论显然是错误
这是因为 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
下列推理是归纳推理的是
A.已知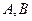 为定点,动点 为定点,动点 满足 满足 ,得动点 ,得动点 的轨迹为椭圆 的轨迹为椭圆 |
B.由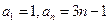 求出 求出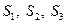 ,猜想出数列的前 ,猜想出数列的前 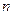 项和 项和 的表达式 的表达式 |
C.由圆 的面积为 的面积为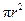 ,猜想出椭圆 ,猜想出椭圆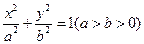 的面积为 的面积为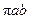 |
| D.科学家利用鱼的沉浮原理制造潜水艇 |
试题篮
()