下面几种推理过程是演绎推理的是
A.两条直线平行,同旁内角互补,如果 和 和 是两条平行线的同旁内角,则 是两条平行线的同旁内角,则 ; ; |
| B.由平面三角形的性质,推测空间四面体的性质; |
| C.某校共有10个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人; |
D.在数列 中, 中, ,由此归纳出 ,由此归纳出 的通项公式. 的通项公式. |
下列几种推理是演绎推理的是( )
A.在数列 中, 中, ,由此归纳出 ,由此归纳出 的通项公式 的通项公式 |
| B.某高校高三(1)班有55人,(2)班有54人,(3)班有52人,由此得出高三所有班级的人数都超过50人。 |
| C.由平面三角形的性质,推测出空间四面体的性质 |
D.两条直线平行,同旁内角互补。如果 是两条直线的同旁内角,则 是两条直线的同旁内角,则 |
.已知①正方形的对角线相等,②矩形的对角线相等,③正方形是矩形。根据“三段论”推理出一个结论,则这个结论是 ( )
| A.正方形的对角线相等 | B.矩形的对角线相等 | C.正方形是矩形 | D.其它 |
已知①正方形的对角线相等;②矩形的对角线相等;③正方形是矩形.根据”三段论”推理出一个结论。则这个结论是( )
| A.正方形的对角线相等 | B.矩形的对角线相等 | C.正方形是矩形 | D.其 他 他 |
下面几种推理过程是演绎推理的是( )
A.两条直线平行,同旁内角互补,如果 与 与 是两条平行直线的同旁内角,则 是两条平行直线的同旁内角,则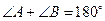 。 。 |
| B.某校高二(1)班有55人,高二(2)班有52人,由此得高二所有班人数超过50人。 |
C. 由平面三角形的性质,推出空间四边形的性质。 由平面三角形的性质,推出空间四边形的性质。 |
D.在数列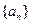 中, 中,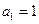 , ,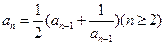 ,通过计算 ,通过计算 , , , , 由此归纳出 由此归纳出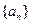 的通项公式。 的通项公式。 |
命题“有理数是无限循环小数,整数是有 理数,所以整数是无限循环小数”是假命题,推理错误的原因是( )
理数,所以整数是无限循环小数”是假命题,推理错误的原因是( )
| A.使用了归纳推理 | B.使用类比推理 |
| C.使用三段论,但大前提错误 | D.使用三段论,但小前提错误 |
一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示. 某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断:① 0点到3点只进水不出水; ②3点到4点不进水只出水; ③4点到6点不进水不出水. 则正确论断的个数是( )
| A.3 | B.2 | C.1 | D. 0 |

试题篮
()