高中数学合情推理和演绎推理选择题

将个正整数、、、 、（）任意排成行列的数表．对于某一个数表,计算各行和各列中的任意两个数、（）的比值,称这些比值中的最小值为这个数表的“特征值”．当时,数表的所有可能的“特征值”最大值为（  ）

A．

B．

C．

D．

下列推理中属于归纳推理且结论正确的是（　　）

A．由an=2n﹣1，求出S1=1^2，S2=2^2，S3=3^2，…，推断：数列{an}的前n项和Sn=n^2

B．由f（x）=xcosx满足f（﹣x）=﹣f（x）对都成立，推断：f（x）=xcosx为奇函数

C．由圆x^2+y^2=r^2的面积S=πr^2，推断：椭圆=1的面积S=πab

D．由，…，推断：对一切，（n+1）^2＞2^n

已知（），计算得，，，，，由此推算：当时，有（   ）

A．（）

B．（）

C．（）

D．（）

给出命题：若是正常数，且，，则(当且仅当时等号成立)．根据上面命题，可以得到函数（）的最小值及取最小值时的值分别为（   ）

A．，	B．，
C．25，	D．，

二维空间中圆的一维测度（周长），二维测度（面积），观察发现；三维空间中球的二维测度（表面积），三维测度（体积），观察发现．则四维空间中“超球”的三维测度，猜想其四维测度W=      ．

六个面都是平行四边形的四棱柱称为平行六面体。如，在平行四边形中，有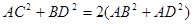，那么在图（2）的平行六面体中有等于(  )

A．	B．
C．	D．

记，当时，观察下列等式：
，
，
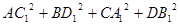，可以推测A-B等于（   ）

A．

B．

C．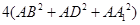

D．

对于任意正整数n，定义“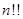”如下：
当n是偶数时，，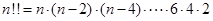
当n是奇数时，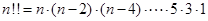
现在有如下四个命题：
①；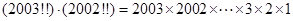
②；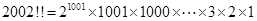
③的个位数是0；
④的个位数是5。
其中正确的命题有（   ）

A．1个

B．2个

C．3个

D．4个

面积为S的平面凸四边形的第条边的边长记为，此四边形内任一点P到第条边的距离记为，若，则．类比以上性质，体积为V的三棱锥的第个面的面积记为，此三棱锥内任一点Q到第个面的距离记为，若，则等于（   ）

A．

B．

C．

D．

定义：分子为1且分母为正整数的分数称为单位分数．我们可以把1分拆为若干个不同的单位分数之和．如：，，， 
依此类推可得：，
其中，．设，则的最小值为（   ）

A．

B．

C．

D．

三段论推理“①矩形是平行四边形；②三角形不是平行四边形；③三角形不是矩形”中的小前提是(　　)

A．①

B．②

C．③

D．①和②

已知“整数对”按如下规律排成一列：(1,1)，(1,2)，(2,1)，(1,3)，(2,2)，(3,1)，(1,4)，(2,3)，(3,2)，(4,1)，…，则第60个“整数对”是(　　)

A．(7,5)

B．(5,7)

C．(2,10)

D．(10,1)

设△ABC的三边长分别为a，b，c，△ABC的面积为S，内切圆半径为r，则r＝，类比这个结论可知：四面体S—ABC的四个面的面积分别为S₁，S₂，S₃，S₄，内切球半径为R，四面体S—ABC的体积为V，则R等于

A．	B．
C．	D．

如图所示，面积为的平面凸四边形的第条边的边长记为（），此四边形内任一点到第条边的距离记为（），若，则．类比以上性质，体积为的三棱锥的第个面的面积记为（），此三棱锥内任一点到第个面的距离记为（），若，则等于（   ）

A．

B．

C．

D．

如图所示，面积为的平面凸四边形的第条边的边长记为（），此四边形内任一点到第条边的距离记为（），若，则．类比以上性质，体积为的三棱锥的第个面的面积记为（），此三棱锥内任一点到第个面的距离记为（），若，则等于

A．

B．

C．

D．