高中数学合情推理和演绎推理试题

在平面直角坐标系上，设不等式组所表示的平面区域为，记内的整点（即横坐标和纵坐标均为整数的点）的个数为．则＝         ，经猜想可得到＝         ．

设数列的前n项的和与的关系是.
（1）求并归纳出数列的通项（不需证明）；
（2）求数列的前项和.

在△ABC中，若D为BC 的中点，则有，将此结论类比到四面体中，在四面体 A-BCD中，若G为△BCD的重心，则可得一个类比结论：     ．

（本小题满分10分）
（Ⅰ）证明：．
（Ⅱ）已知圆的方程是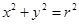，则经过圆上一点的切线方程为：
，类比上述性质，试写出椭圆类似的性质．

对于实数，表示不超过的最大整数，观察下列等式：

按照此规律第个等式的等号右边的结果为               ．

古希腊毕达哥拉斯学派的数学家研究过各种多边形数．如三角形数1,3,6,10，…，第个三角形数为．记第个边形数为，以下列出了部分边形数中第个数的表达式：
三角形数    
正方形数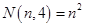     
五边形数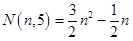     
六边形数     
……
可以推测的表达式，由此计算        ．

如图所示，面积为的平面凸四边形的第条边的边长记为（），此四边形内任一点到第条边的距离记为（），若，则．类比以上性质，体积为的三棱锥的第个面的面积记为（），此三棱锥内任一点到第个面的距离记为（），若，则等于（   ）

A．

B．

C．

D．

（本小题满分16分）图（1）、（2）、（3）、（4）分别包含1个、5个、13个、25个第二十九届北京奥运会吉祥物“福娃迎迎”，按同样的方式构造图形，设第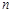个图形包含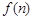个“福娃迎迎”．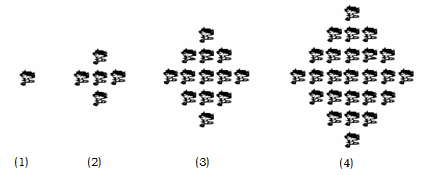

（1）求出；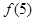
（2）利用合情推理的“归纳推理思想”归纳出与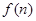的关系式（不需写出证明过程）；
（3）根据你得到的关系式求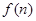的表达式．

对于实数，表示不超过的最大整数，观察下列等式：

按照此规律第个等式的等号右边的结果为               ．

古希腊毕达哥拉斯学派的数学家研究过各种多边形数。如三角形数1,3,6,10，第n个三角形数为． 记第n个k边形数为N（n，k）（，以下列出了部分k边形数中第n个数的表达式：
三角形数            
四边形数            
五边形数            
六边形数            
……
可以推测的表达式，由此计算的值为_____________．

分形是几何学是美籍法国数学家伯努瓦·曼德尔布罗（BenoitMandelbrot）在20世纪70年代创立的一门新学科，它的创立为解决传统科学众多领域的难题提供了全新的思路．按照下图1的分形规律可得到如图2所示的一个树形图，则当时，第行空心圆点个数与第行及第行空心圆点个数的关系式为________；第12行的实心圆点的个数是_______．

记，当时，观察下列等式：
，，，，， ，可以推测           ．

在中，三个内角A、B、C的对边分别为a,b,c，且A、B、C成等差数列，a,b,c成等比数列，请用分析法证明：为等边三角形。

如图所示，面积为的平面凸四边形的第条边的边长记为（），此四边形内任一点到第条边的距离记为（），若，则．类比以上性质，体积为的三棱锥的第个面的面积记为（），此三棱锥内任一点到第个面的距离记为（），若，则等于

A．

B．

C．

D．

面积为S的平面凸四边形的第条边的边长记为，此四边形内任一点P到第条边的距离记为，若，则．类比以上性质，体积为V的三棱锥的第个面的面积记为，此三棱锥内任一点Q到第个面的距离记为，若，则等于（   ）

A．

B．

C．

D．