现有一个关于平面图形的命题,如图所示,同一个平面内有两个边长都是 的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为
的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为 .类比到空间,有两个棱长均为
.类比到空间,有两个棱长均为 的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
如图,在正三角形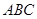 中,
中,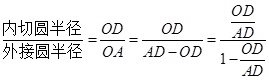 ,
,
而 ,所以
,所以 。应用类比推理,在正四面体
。应用类比推理,在正四面体 (每个面都是正三角形的四面体)中,
(每个面都是正三角形的四面体)中,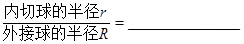 。
。
数列 的前n项和为
的前n项和为 ,若数列
,若数列 的各项按如下规律排列:
的各项按如下规律排列:
有如下运算和结论:① ②数列
②数列 是等比
是等比
数列;③数列 的前n项和为
的前n项和为 ④若
④若
存在正整数 ,使
,使 其中正确的结论有 .(将你认
其中正确的结论有 .(将你认
为正确的结论序号都填上)
设面积为 的平面四边形的第
的平面四边形的第 条边的边长记为
条边的边长记为 ,
, 是该四边形内任意一点,
是该四边形内任意一点, 点到第
点到第 条边的距离记为
条边的距离记为 ,若
,若 , 则
, 则 类比上述结论,体积为
类比上述结论,体积为 的三棱锥的第
的三棱锥的第 个面的面积记为
个面的面积记为 ,
, 是该三棱锥内的任意一点,
是该三棱锥内的任意一点, 点到第
点到第 个面的距离记为
个面的距离记为 ,则相应的正确命题是:若
,则相应的正确命题是:若 ,则 .
,则 .
某校数学课外小组在坐标纸上为学校的一块空地设计植树方案如下:第 棵树种植在点
棵树种植在点 处,其中
处,其中 ,当
,当 时,
时,
 表示非负实数
表示非负实数 的整数部分,例如
的整数部分,例如
按此方案,第2012棵树种植点的坐标应为_________________.
把数列 依次按第一个括号一个数,第二个括号两
依次按第一个括号一个数,第二个括号两
个数,第三个括号三个数,第四个括号四个数,……按此规律下去,
即( ),(
),( ,
, ),(
),( ,
,  ,
, ),(
),( ,
, ,
, ,
, ),
),
则第6个括号内各数字之和为 .
在平面几何中,有射影定理:“在 中,
中, ,点
,点 在
在 边上的射影为
边上的射影为 ,有
,有 .”类比平面几何定理,研究三棱锥的侧面面积与射影面积、底面面积的关系,可以得出的正确结论是:“在三棱锥
.”类比平面几何定理,研究三棱锥的侧面面积与射影面积、底面面积的关系,可以得出的正确结论是:“在三棱锥 中,
中, 平面
平面 ,点
,点 在底面
在底面 上的射影为
上的射影为 ,则有 .”
,则有 .”
若 三边长分别为
三边长分别为 、
、 、
、 ,内切圆的半径为
,内切圆的半径为 ,则
,则 的面积
的面积 ,类比上述命题猜想:若四面体
,类比上述命题猜想:若四面体 四个面的面积分别为
四个面的面积分别为 、
、 、
、 、
、 ,内切球的半径为
,内切球的半径为 ,则四面体
,则四面体 的体积
的体积
在直角三角形ABC中,CA⊥CB,斜边AB上的高为h1,则  类比此性质,在四面体P-ABC中,若PA,PB,PC两两垂直底面ABC上的高为h,则得到的正确结论________.
类比此性质,在四面体P-ABC中,若PA,PB,PC两两垂直底面ABC上的高为h,则得到的正确结论________.
如图,将一个边长为1的正三角形的每条边三等分,以中间一段为边向形外作正三角形,并擦去中间一段,得图(2),如此继续下去,得图(3)……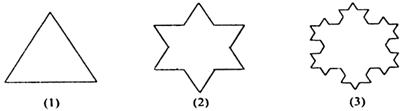
试用 n表示出第n个图形的边数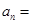
试题篮
()