在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面
ABCD,AE⊥BD,CB=CD=CF=1,
(1)求证:BD⊥平面AED;
(2)求B到平面FDC的距离.
如图,四边形ABCD为正方形,PD⊥平面ABCD, ,AF⊥PC于点F,FE∥CD交PD于点E.
,AF⊥PC于点F,FE∥CD交PD于点E.
(1)证明:CF⊥平面ADF;
(2)若 ,证明
,证明 平面
平面
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在弧AB上,且OM∥AC.
(1)求证:平面MOE∥平面PAC.
(2)求证:平面PAC⊥平面PCB.
(3)设二面角M—BP—C的大小为θ,求cos θ的值.
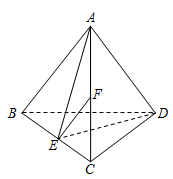
(本小题满分14分)如图,在四面体 中,
中, ,点
,点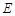 是
是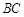 的中点,点
的中点,点 在线段
在线段 上,且
上,且 .
.
(1)若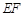 ∥平面
∥平面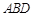 ,求实数
,求实数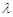 的值;
的值;
(2)求证:平面 平面
平面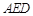 .
.
如图,直三棱柱 中,
中, 、
、 分别是棱
分别是棱 、
、 的中点,点
的中点,点 在棱
在棱 上,已知
上,已知 ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)设点 在棱
在棱 上,当
上,当 为何值时,平面
为何值时,平面 平面
平面 ?
?
(本小题满分12分)在如图所示的几何体中, 与
与 都是边长为2的等比三角形且所在平面互相平行,四边形BCED为正方形,
都是边长为2的等比三角形且所在平面互相平行,四边形BCED为正方形, ,O,G分别是BC,DE的中点.
,O,G分别是BC,DE的中点.
(1)证明:平面ADE 平面AOFG;
平面AOFG;
(2)求二面角D-AE-F的余弦值.
如图,在四棱柱ABCD-A1B1C1D1中,已知平面AA1C1C丄平面ABCD,且AB=BC=CA= ,AD=CD=1.
,AD=CD=1.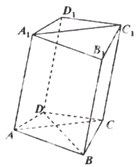
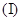 求证:BD⊥AA1;
求证:BD⊥AA1; 若四边形
若四边形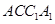 是菱形,且
是菱形,且 ,求四棱柱
,求四棱柱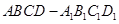 的体积.
的体积.
(本小题满分13分)
如图,⊙O在平面 内,AB是⊙O的直径,
内,AB是⊙O的直径, 平面
平面 ,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)求证: 平面
平面 .
.
(本小题满分14分)如图,在五面体 中,四边形
中,四边形 为正方形,
为正方形, ,平面
,平面
 平面
平面 ,且
,且 ,
, ,点G是EF的中点.
,点G是EF的中点.
(Ⅰ)证明:

 ;
;
(Ⅱ)若点 在线段
在线段 上,且
上,且 ,求证:
,求证: //平面
//平面 ;
;
(Ⅲ)已知空间中有一点O到 五点的距离相等,请指出点
五点的距离相等,请指出点 的位置. (只需写出结论)
的位置. (只需写出结论)
(本小题满分14分)
如图,四边形 是正方形,△
是正方形,△ 与△
与△ 均是以
均是以 为直角顶点的等腰直角三角形,点
为直角顶点的等腰直角三角形,点 是
是 的中点,点
的中点,点 是边
是边 上的任意一点.
上的任意一点.
(1)求证: ;
;
(2)求二面角 的平面角的正弦值.
的平面角的正弦值.
如图所示,已知 为圆
为圆 的直径,点
的直径,点 为线段
为线段 上一点,且
上一点,且 ,点
,点 为圆
为圆 上一点,且
上一点,且 .点
.点 在圆
在圆 所在平面上的正投影为点
所在平面上的正投影为点 ,
, .
.
(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
试题篮
()