如图,在四棱锥 中,已知底面
中,已知底面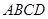 为矩形,
为矩形, 平面
平面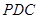 ,点
,点 为棱
为棱 的中点,求证:
的中点,求证:
(1) 平面
平面 ;
;
(2)平面 平面
平面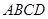 .
.
如图,已知直三棱柱 的侧面
的侧面 是正方形,点
是正方形,点 是侧面
是侧面 的中心,
的中心, ,
, 是棱
是棱 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 .
.
如图,三棱柱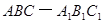 中,
中, 平面ABC,AB
平面ABC,AB BC , 点M , N分别为A1C1与A1B的中点.
BC , 点M , N分别为A1C1与A1B的中点.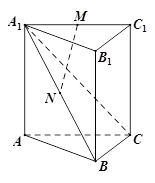
(Ⅰ)求证:MN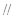 平面BCC1B1;
平面BCC1B1;
(Ⅱ)求证:平面A1BC 平面A1ABB1.
平面A1ABB1.
如图,直三棱柱ABC﹣A′B′C′,∠BAC=90°, ,AA′=1,点M,N分别为A′B和B′C′的中点.
,AA′=1,点M,N分别为A′B和B′C′的中点.
(Ⅰ)证明:MN∥平面A′ACC′;
(Ⅱ)求三棱锥A′﹣MNC的体积.
(椎体体积公式V= Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高)
如图,在正方体ABCD﹣A1B1C1D1中,E,F,G,M,N分别是B1C1,A1D1,A1B1,BD,B1C的中点,求证:
(1)MN∥平面CDD1C1.
(2)平面EBD∥平面FGA.
试题篮
()