(本小题满分12分)
用半径为R的圆形铁皮剪出一个圆心角为α的扇形,制成一个圆锥形容器,求:扇形的.圆心角多大时,容器的容积最大?并求出此时容器的最大容积.
建立适当的坐标系,用坐标法解决下列问题:
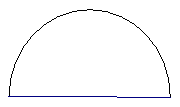
已知隧道的截面是半径为4m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7m,高为3m的货车能不能驶入这个隧道?
 |
如图,在四边形ABCD中,AD=8,CD=6,AB=13,∠ADC=90°,且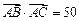 .
.
(1)求sin∠BAD的值;
(2)设△ABD的面积为S△ABD,△BCD的面积为S△BCD,求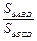 的值.
的值.
 |
如图,圆 内有一点
内有一点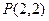 ,过点
,过点 作直线
作直线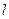 交圆于
交圆于 两点.(1)当直线
两点.(1)当直线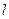 经过圆心
经过圆心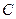 时,求直线
时,求直线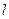 的方程;(2)当弦
的方程;(2)当弦 被点
被点 平分时,写出直线
平分时,写出直线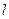 方程;(3)当直线
方程;(3)当直线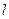 倾斜角为
倾斜角为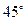 时,求
时,求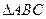 的面积.
的面积.

已知动圆过定点P(1,0),且与定直线 相切,点C在
相切,点C在 上.
上.
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且斜率为- 的直线与曲线M相交于A、B两点,
的直线与曲线M相交于A、B两点,
①求线段AB的长;
②问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由;
已知半径为5的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
(1)求圆的方程;
(2)设直线 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数 ,使得过点
,使得过点 的直线
的直线 垂直平分弦
垂直平分弦 ?
?
存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
试题篮
()