高中数学随机思想的发展试题

随机变量的分布列如下：

 
其中成等差数列，若，则的值是         ;

（本小题满分12分）
现有甲、乙两个口袋，甲袋装有2个红球和2个白球，乙袋装有2个红球和n个白球，某人从甲、乙两个口袋中等可能性地各取2个球．
（1）若，求取到的4个球全是红球的概率；
（2）若取到的4个球中至少有2个红球的概率为，求n的值．

从4名男生和2名女生中任选3人参加辩论比赛，设随机变量表示所选3人中女生的人数，则的数学期望为        .

（理）袋中有同样的球个，其中个红色，个黄色，现从中随机且不返回地摸球，每次摸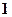个，当两种颜色的球都被摸到时，即停止摸球，记随机变量为此时已摸球的次数，求：.
(1)随机变量的概率分布律；
(2)随机变量的数学期望与方差.

已知100件产品中有10件次品，从中任取3件，则任意取出的3件产品中次品数的数学期望为　　　，方差为　　，

(本小题满分12分)
一个袋子内装有若干个黑球，个白球，个红球（所有的球除颜色外其它均相同），从中任取个球，每取得一个黑球得分，每取一个白球得分，每取一个红球得分，已知得分的概率为，用随机变量X表示取个球的总得分.
（Ⅰ）求袋子内黑球的个数；
（Ⅱ）求X的分布列.

(本小题满分12分)
已知盒子中有六张分别标有数字1、2、3、4、5、6的卡片
（Ⅰ）现从盒子中任取两张卡片，将卡片上的数字相加，求所得数字是奇数的概率；
（Ⅱ）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张标有数字为偶数的卡片则停止抽取，否则继续进行，求抽取次数的分布列．

（本小题满分12分）
甲、乙两人进行一场乒乓球比赛，根据以往比赛的胜负情况知道，每一局比赛甲胜的概率0.6，乙胜的概率为0.4，本场比赛采用三局两胜制。
（1）求甲获胜的概率.
（2）设ξ为本场比赛的局数，求ξ的概率分布和数学期望.

在上海世界博览会开展期间，计划选派部分高二学生参加宣传活动，报名参加的学生需进行测试，共设4道选择题，规定必须答完所有题，且答对一题得1分，答错一题扣1分，至少得2分才能入选成为宣传员；甲乙丙三名同学报名参加测试，他们答对每个题的概率都为，且每个人答题相互不受影响.
（1）用随机变量表示能够成为宣传员的人数，求的数学期望与方差；
（2）若学生甲得分的数值为随机变量，求所得分数的分布列和数学期望.

已知离散型随机变量的概率分布如下：

	0	1	2
P	0.3	3k	4k

随机变量，则的数学期望为(    )

A．1.1

B．3.2

C．11k

D．22k+1

在某次数学考试中，考生的成绩，则考试成绩X位于区间(80,90)上的概率为      。

设一随机试验的结果只有和，且，令随机变量，则的方差等于（     ）

A．

B．

C．

D．

已知随机变量，则与分别为（    ）

A．2.4 4

B．6 2.4

C．4 2.4

D．6 4

某家具城进行促销活动，促销方案是：顾客每消费满1000元，便可以获得奖券一张，每张奖券
中奖的概率为，若中奖，则家具城返还顾客现金1000元，某顾客购买一张价格为3400元的餐桌，
得到3张奖券，设该顾客购买餐桌的实际支出为元；
（I）求的所有可能取值；
（II）求的分布列；
（III）求的期望E（）；

某射击运动员为争取获得2010年广州亚运会的参赛资格正在加紧训练.已知在某次训练中他射击了枪，每一枪的射击结果相互独立，每枪成绩不低于10环的概率为，设为本次训练中成绩不低于10环的射击次数，的数学期望，方差.
（1）求的值；
（2）训练中教练要求：若有5枪或5枪以上成绩低于10环，则需要补射，求该运动员在本次训练中需要补射的概率.
（结果用分数表示.已知：，）