已知随机变量 的分布列为下表所示:
的分布列为下表所示:
 |
1 |
3 |
5 |
| P |
0.4 |
0.1 |
 |
则 的标准差为( )
的标准差为( )
A.3.56 B. C.3.2 D.
C.3.2 D.
某产品按行业生产标准分成 个等级,等级系数
个等级,等级系数 依次为
依次为 ,其中
,其中 为标准
为标准 ,
, 为标准
为标准 ,产品的等级系数越大表明产品的质量越好. 已知某厂执行标准
,产品的等级系数越大表明产品的质量越好. 已知某厂执行标准 生产该产品,且该厂的产品都符合相应的执行标准.从该厂生产的产品中随机抽取
生产该产品,且该厂的产品都符合相应的执行标准.从该厂生产的产品中随机抽取 件,相应的等级系数组成一个样本,数据如下:
件,相应的等级系数组成一个样本,数据如下:
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
该行业规定产品的等级系数 的为一等品,等级系数
的为一等品,等级系数 的为二等品,等级系数
的为二等品,等级系数 的为三等品.
的为三等品.
(1)试分别估计该厂生产的产品的一等品率、二等品率和三等品率;
(2)从样本的一等品中随机抽取2件,求所抽得2件产品等级系数都是8的概率
“剪刀、石头、布”游戏的规则是:出拳之前双方齐喊口令,然后在话音刚落时同时出拳,握紧的拳头代表“石头”,食指和中指伸出代表“剪刀”,五指伸开代表“布”.“石头”胜“剪刀”, “剪刀”胜“布”,而“布”又胜“石头”,如果所出的拳相同,则为和局.现甲乙二人通过“剪刀、石头、布”游戏进行比赛.
(Ⅰ) 设甲乙二人每局都随机出“剪刀”、“石头”、“布”中的某一个,求甲胜乙的概率;
(Ⅱ)据专家分析,乙有以下的出拳习惯:① 第一局不出“剪刀”;② 连续两局的出拳方法一定不一样,即如果本局出“剪刀”,则下局将不再出“剪刀”,而是选“石头”、“布”中的某一个.假设专家的分析是正确的,甲根据专家的分析出拳,保证每一局都不输给乙.在最多5局的比赛中,谁胜的局数多,谁获胜.游戏结束的条件是:一方胜3局或赛满5局,用X表示游戏结束时的游戏局数,求X的分布列和期望.
乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用 局
局 胜制(即先胜
胜制(即先胜 局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(Ⅰ)求甲以 比
比 获胜的概率;
获胜的概率;
(Ⅱ)求乙获胜且比赛局数多于 局的概率;
局的概率;
(Ⅲ)求比赛局数的分布列.
六名学生需依次进行身体体能和外语两个项目的训练及考核。每个项目只有一次补考机会,补考不合格者不能进入下一个项目的训练(即淘汰),若每个学生身体体能考核合格的概率是 ,外语考核合格的概率是
,外语考核合格的概率是 ,假设每一次考试是否合格互不影响。
,假设每一次考试是否合格互不影响。
①求某个学生不被淘汰的概率。
②求6名学生至多有两名被淘汰的概率
③假设某学生不放弃每一次考核的机会,用 表示其参加补考的次数,求随机变量
表示其参加补考的次数,求随机变量 的分布列和数学期望。
的分布列和数学期望。
(本小题满分12分)
某产品按行业生产标准分成 个等级,等级系数
个等级,等级系数 依次为
依次为 ,其中
,其中 为标准
为标准 ,
, 为标准
为标准 ,产品的等级系数越大表明产品的质量越好. 已知某厂执行标准
,产品的等级系数越大表明产品的质量越好. 已知某厂执行标准 生产该产品,且该厂的产品都符合相应的执行标准.从该厂生产的产品中随机抽取
生产该产品,且该厂的产品都符合相应的执行标准.从该厂生产的产品中随机抽取 件,相应的等级系数组成一个样本,数据如下:
件,相应的等级系数组成一个样本,数据如下:
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
该行业规定产品的等级系数 的为一等品,等级系数
的为一等品,等级系数 的为二等品,等级系数
的为二等品,等级系数 的为三等品.
的为三等品.
(1)试分别估计该厂生产的产品的一等品率、二等品率和三等品率;
(2)从样本的一等品中随机抽取2件,求所抽得2件产品等级系数都是8的概率.
假设某次数学测试共有20道选择题,每个选择题都给了4个选项(其中有且仅有一个是正确的)。评分标准规定:每题只选1项,答对得5分,否则得0分。某考生每道题都给出了答案,并且会做其中的12道题,其他试题随机答题,则他的得分X的方差DX=
将编号为1到4的4个小球放入编号为1到4的4个盒子,每个盒子放1个球,记随机变量 为小球编号与盒子编号不一致的数目,则
为小球编号与盒子编号不一致的数目,则 的数学期望是 ▲ ;
的数学期望是 ▲ ;
袋中装有13个红球和 个白球,这些红球和白球除了颜色不同之外,其余都相同,从袋中同时取两个球.
个白球,这些红球和白球除了颜色不同之外,其余都相同,从袋中同时取两个球.
(1)若取出的是2个红球的概率等于取出的是一红一白两个球的概率的3倍,试求 的值;
的值;
(2) 某公司的某部门有21位职员,公司将进行抽奖活动,在(1)的条件下,规定:每个职员都从袋中同时取两个球,然后放回袋中,摇匀再给别人抽奖,若某人取出的两个球是一红一白时,则中奖(奖金1000元);否则,不中奖(也发鼓励奖金100元).试求此公司在这次抽奖活动中所发奖金总额的期望值.
.【必做题】本题满分10分.解答时应写出文字说明、证明过程或演算步骤.
由数字1,2,3,4组成五位数 ,从中任取一个.
,从中任取一个.
(1)求取出的数满足条件:“对任意的正整数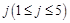 ,至少存在另一个正整数
,至少存在另一个正整数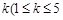 ,且
,且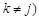 ,使得
,使得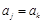 ”的概率;
”的概率;
(2)记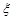 为组成该数的相同数字的个数的最大值,求
为组成该数的相同数字的个数的最大值,求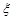 的概率分布列和数学期望.
的概率分布列和数学期望.
某商场“五一”期间举行有奖促销活动,顾客只要在商店购物满800元就能得到一次摸奖机会.摸奖规则是:在盒子内预先放有5个大小相同的球,其中一个球标号是0,两个球标号都是40,还有两个球没有标号。顾客依次从盒子里摸球,每次摸一个球(不放回),若累计摸到两个没有标号的球就停止摸球,否则将盒子内球摸完才停止.奖金数为摸出球的标号之和(单位:元),已知某顾客得到一次摸奖机会。
(1)求该顾客摸三次球被停止的概率;
(2)设 为该顾客摸球停止时所得的奖金数,求
为该顾客摸球停止时所得的奖金数,求 的分布列及均值.
的分布列及均值.
试题篮
()