高中数学随机思想的发展试题

某高校设计了一个实验学科的实验考查方案：考生从6道备选题中一次性随机抽取3题，按照题目要求独立完成全部实验操作； 其中6道备选题中考生甲有4题能正确完成，2题不能完成，则甲考生能正确完成题数的数学期望为               

将3个小球随机地放入3个盒子中，记放有小球的盒子个数为X，则X的均值　　　　．

某校的学生记者团由理科组和文科组构成，具体数据如下表所示：

组别	理科	文科
性别	男生	女生	男生	女生
人数	4	4	3	1

学校准备从中选出4人到社区举行的大型公益活动进行采访，每选出一名男生，给其所在小组记1分，每选出一名女生则给其所在小组记2分，若要求被选出的4人中理科组、文科组的学生都有．(Ⅰ)求理科组恰好记4分的概率？
(Ⅱ)设文科男生被选出的人数为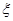，求随机变量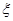的分布列和数学期望．

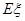某项新技术进入试用阶段前必须对其中三项不同指标甲、乙、丙进行通过量化检测。假设该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为，指标甲、乙、丙检测合格分别记4分、2分、4分，若某项指标不合格，则该项指标记0分，各项指标检测结果互不影响。
（Ⅰ）求该项技术量化得分不低于8分的概率；
（Ⅱ）记该技术的三个指标中被检测合格的指标个数为随机变量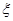，求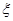的分布列与数学期望。

口袋中有5只球，编号为1，2，3，4，5，从中任取3球，以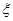表示取出的球的最大号码，则(　   　)

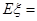A． 4

B． 5

C．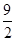

D．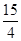

河南省某示范性高中为了推进新课程改革，满足不同层次学生的需求，决定从高一年级开始，在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座，每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座，也可以放弃任何一门科目的辅导讲座（规定：各科达到预先设定的人数时称为满座，否则称为不满座）．统计数据表明，各学科讲座各天的满座概率如下表：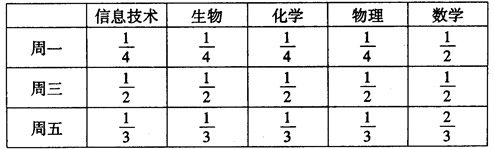

（Ⅰ）求数学辅导讲座在周一、周三、周五都不满座的概率；
（Ⅱ）设周三各辅导讲座满座的科目数为ξ，求随机变量ξ的分布列和数学期望．

甲、乙两名工人加工同一种零件，两人每天加工的零件数相等，所出次品数分别为，，且和的分布列为：

	0	1	2

 
试比较两名工人谁的技术水平更高．

学校为绿化环境，移栽了甲、乙两种大树各2株．设甲、乙两种大树移栽的成活率分别为和，且各株大树是否成活互不影响．
（Ⅰ）求移栽的4株大树中恰有3株成活的概率；
（Ⅱ）设移栽的4株大树中成活的株数为,求分布列与期望．

已知函数
（Ⅰ）若，求函数有零点的概率；
（Ⅱ）若是区间上的两个均匀随机数，求函数有零点的概率

如果甲乙两个乒乓球选手进行比赛，而且他们在每一局中获胜的概率都是，规定使用“七局四胜制”，即先赢四局者胜．
(1)试分别求甲打完4局、5局才获胜的概率；
(2)设比赛局数为ξ，求ξ的分布列及期望．

(8分) 出租车司机从饭店到火车站途中有六个交通岗，假设他在各交通岗到红灯这一事件是相互独立的，并且概率都是
（I）求这位司机遇到红灯前，已经通过了两个交通岗的概率；
（II）求这位司机在途中遇到红灯数ξ的期望和方差。

设是离散型随机变量，，，且a<b，又Eξ=，Dξ=，则a+b的值为（  ）

A．

B．

C．3

D．

某班有名同学，一次考试后的数学成绩服从正态分布，则理论上分到 分的人数是 (     ) 

A．32

B．16

C．8

D．20

某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如下：

（1）比较这两名队员在比赛中得分的均值和方差的大小；
（2）以上述数据统计甲、乙两名队员得分超过15分的频率作为概率，假设甲、乙两名队员在同一场比赛中得分多少互不影响，预测在本赛季剩余的2场比赛中甲、乙两名队员得分均超过15分的次数的分布列和均值．

有5支竹签编号分别为1,2,3,4,5，从中任取3支，以表示取出的竹签的最大号码，则的值是 .