某校甲、乙两个班级各有5名编号为1，2，3，4，5的学生进行投篮训练，每人投10次，投中的次数统计如下表：
| 学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
| 甲班 |
6 |
5 |
7 |
9 |
8 |
| 乙班 |
4 |
8 |
9 |
7 |
7 |
（1）从统计数据看，甲、乙两个班哪个班成绩更稳定（用数字特征说明）；
（2）若把上表数据作为学生投篮命中率，规定两个班级的1号和2号同学分别代表自己的班级参加比赛，每人投篮一次，将甲、乙两个班两名同学投中的次数之和分别记作
和
，试求和的分布列和数学期望．
（本小题满分12分）已知一个袋子中有3个白球和3个红球，这些球除颜色外完全相同．
（Ⅰ）每次从袋中取出一个球，取出后不放回，直到取到一个红球为止，求取球次数
的分布列和数学期望
；
（Ⅱ）每次从袋中取出一个球，取出后放回接着再取一个球，这样取3次，求取出红球次数
的数学期望
．
某单位在公开招收公务员考试时，笔试阶段须对报考人员进行三个项目的测试．规定三项都合格者笔试通过．假定每项测试相互独立，报考人员甲各项测试合格的概率组成一个公比为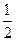
的等比数列，第一项测试合格且第二项测试也合格的概率为
．
（1）求报考人员甲笔试通过的概率；
（2）求报考人员甲测试合格的项数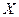
的分布列和数学期望．
（本小题满分12分）
2010年
上海世博会大力倡导绿色出行，并提出在世博园区参观时可以通过植树的方式来抵消因出行产生的碳排放量，某游客计划在游园期间种植n棵树，已知每棵树是否成活互不影响，成活率都为
，用
表示他所种植的树中成活的棵数，的数学期望为E，方差为D。
（I） 若n=1，求D的最大值；
（II） 已知E=3，标准差
，试求n与p的值并写出的分布列。
（本小题满分12分）
甲、乙两人各射击一次，击中目标的概率分别是
和
假设两人射击是否击中目标，相互
之间没有影响；每人各次射击是否击中目标，相互之间也没有影响
（1）甲射击3次，至少1次未击中目标的概率；
（2）假设某人连续2次未击中目标，则停止射击，问：乙恰好射击4次后，被中止射击的概率是多少？
⑶设甲连续射击3次，用
表示甲击中目标时射击的次数，求的数学期望
.（结果可以用分数表示）
2011年深圳大运会，某运动项目设置了难度不同的甲、乙两个系列，每个系列都有K和D两个动作，比赛时每位运动员自选一个系列完成，两个动作得分之和为该运动员的成绩。假设每个运动员完成每个系列中的两个动作的得分是相互独立的，根据赛前训练统计数据，某运动员完成甲系列和乙系列的情况如下表：
甲系列：
| 动作 |
K |
D |
||
| 得分 |
100 |
80 |
40 |
10 |
| 概率 |
 |
 |
|
|
乙系列：
| 动作 |
K |
D |
||
| 得分 |
90 |
50 |
20 |
0 |
| 概率 |
 |
 |
|
|
现该运动员最后一个出场，其之前运动员的最高得分为118分。
（I）若该运动员希望获得该项目的第一名，应选择哪个系列，说明理由，并求其获得第一名的概率；
（II）若该运动员选择乙系列，求其成绩X的分布列及其数学期望EX
（本小题满分12分）砷是广泛分布于自然界中的非金属元素， 长期饮用高砷水会直接危害群众的身心健康和生命安全，而近水农村地区，水质情况更需要关注．为了解甲、乙两地区农村居民饮用水中砷含量的基本情况，分别在两地随机选取10个村子，其砷含量的调查数据如下（单位:
）: 
甲地区的10个村子饮用水中砷的含量:
52 32 41 72 43 35 45 61 53 44
乙地区的10个村子饮用水中砷的含量:
44 56 38 61 72 57 64 71 58 62
（Ⅰ）根据两组数据完成下面茎叶图，试比较两个地区中哪个地区的饮用水中砷含量更高，并说明理由；
（Ⅱ）国家规定居民饮用水中砷的含量不得超过50，现医疗卫生组织决定向两个地区中每个砷超标的村子派驻一个医疗救助小组．用样本估计总体，把频率作为概率，若从乙地区随机抽取3个村子，用
表示派驻的医疗小组数，试写出的分布列并求的期望．
一个盒子装有六张卡片，上面分别写着如下六个定义域为R的函数：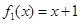
，
，
，
，
，
．
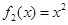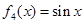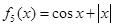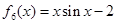（1）现从盒子中任取两张卡片，将卡片上的函数相加得一个新函数，求所得函数是奇函数的概率；
（2）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片则停止抽取，否则继续进行，求抽取次数ξ的分布列和数学期望．
对某班级50名同学一年来参加社会实践的次数进行的调查统计，得到如下频率分布表：
| 参加次数 |
0 |
1 |
2 |
3 |
| 人数 |
0.1 |
0．2 |
0.4 |
0.3 |
根据上表信息解答以下问题：
(1)从该班级任选两名同学，用η表示这两人参加社会实践次数之和，记“函数
在区间
，
内有零点”的事件为
，求发生的概率
；
(2)从该班级任选两名同学，用ξ表示这两人参加社会实践次数之差的绝对值，求随机变量ξ的分布列及数学期望Eξ
口袋里装有大小相同的卡片八张，其中三张标有数字1，三张标有数字2，二张标有数字3，第一次从口袋里任里任意抽取一张，放回口袋里后第二次再任意抽取一张，记第一次与第二次取到卡片上数字之和为
．
（1）为何值时，其发生的概率最大？说明理由；
（2）求随机变量的期望
．
（本小题满分12分）为了进一步激发同学们的学习热情，某班级建立了理科、文科两个学习兴趣小组，两组的人数如下表所示．现采用分层抽样的方法（层内采用简单随机抽样）从两组中共抽取
名同学进行测试．
（Ⅰ）求从理科组抽取的同学中至少有
名女同学的概率；
（Ⅱ）记
为抽取的名同学中男同学的人数，求随机变量的分布列和数学期望．
哈六中体育节进行定点投篮游戏，已知参加游戏的甲、乙两人，他们每一次投篮投中的概率均为
，且各次投篮的结果互不影响．甲同学决定投5次，乙同学决定投中1次就停止，否则就继续投下去，但投篮次数不超过5次．
（1）求甲同学至少有4次投中的概率；
（2）求乙同学投篮次数
的分布列和数学期望．
某理科考生参加自主招生面试，从7道题中（4道理科题3道文科题）不放回地依次任取3道作答．
（1）求该考生在第一次抽到理科题的条件下，第二次和第三次均抽到文科题的概率；
（2）规定理科考生需作答两道理科题和一道文科题，该考生答对理科题的概率均为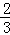
，答对文科题的概率均为
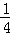，若每题答对得10分，否则得零分．现该生已抽到三道题（两理一文），求其所得总分
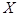的分布列与数学期望
．
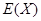甲乙两队参加奥运知识竞赛,每队三人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为
,乙队中三人答对的概率分别为
,且各人回答得正确与否相互之间没有影响.
(1)若用
表示甲队的总得分,求随机变量分布列和数学期望；
(2)用
表示事件“甲、乙两队总得分之和为
”,用
表示事件“甲队总得分大于乙队总得分”,求
.
试题篮
()
粤公网安备 44130202000953号
．
，试写出