高中数学随机思想的发展解答题

据IEC（国际电工委员会）调查显示，小型风力发电项目投资较少，且开发前景广阔，但受风力自然资源影响，项目投资存在一定风险.根据测算，风能风区分类标准如下：

假设投资A项目的资金为（≥0）万元，投资B项目资金为（≥0）万元，调研结果是：未来一年内，位于一类风区的A项目获利的可能性为，亏损的可能性为；位于二类风区的B项目获利的可能性为，亏损的可能性是，不赔不赚的可能性是.
（1）记投资A，B项目的利润分别为和，试写出随机变量与的分布列和期望，；
（2）某公司计划用不超过万元的资金投资于A，B项目，且公司要求对A项目的投
资不得低于B项目,根据（1）的条件和市场调研，试估计一年后两个项目的平均利
润之和的最大值．

经销商经销某种农产品，在一个销售季度内，每售出1 t该产品获利润500元，未售出的产品，每1 t亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了130 t该农产品．以X(单位： t,100≤X≤150)表示下一个销售季度内的市场需求量，T(单位：元)表示下一个销售季度内经销该农产品的利润．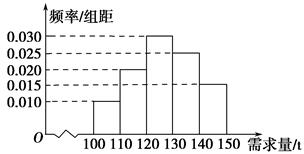

(1)将T表示为X的函数；
(2)根据直方图估计利润T不少于57 000元的概率；
(3)在直方图的需求量分组中，以各组的区间中点值代表该组的各个值，需求量落入该区间的频率作为需求量取该区间中点值的概率(例如：若x∈[100,110)，则取X＝105，且X＝105的概率等于需求量落入[100,110)的频率，求T的数学期望．

（本小题满分12分）从广东省某市高三第一次模拟考试成绩中，随机抽取了名学生的数学成绩得到频率分布直方图如图所示．

（1）根据频率分布直方图，估计该市高三学生本次模拟考试数学成绩的平均分；
（2）以上述样本的频率作为概率，从该市高三学生中有放回地抽取人，记抽到的学生数学成绩不低于
分的人数为，求的分布列和数学期望．

学校游园活动有这样一个游戏项目：甲箱子里装有3个白球，2个黑球，乙箱子里装有1个白球，2个黑球，这些球除颜色外完全相同．每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖(每次游戏结束后将球放回原箱)．
(1)求在1次游戏中：
①摸出3个白球的概率；②获奖的概率．
(2)求在两次游戏中获奖次数X的分布列及数学期望E(X)．

（本小题满分12分）一个盒子中装有大量形状大小一样但重量不尽相同的小球，从中随机抽取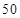个作为样本，称出它们的重量（单位：克），重量分组区间为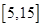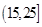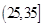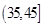，，，，由此得到样本的重量频率分布直方图（如图），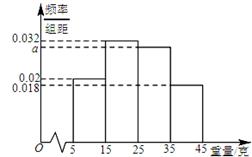

（Ⅰ）求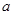的值，并根据样本数据，试估计盒子中小球重量的众数与平均值；
（Ⅱ）从盒子中随机抽取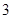个小球，其中重量在内的小球个数为，求的分布列和数学期望. (以直方图中的频率作为概率).

从某批产品中，有放回地抽取产品两次，每次随机抽取1件，假设事件：“取出的2件产品中至多有1件是二等品”的概率．
（Ⅰ）求从该批产品中任取1件是二等品的概率；
（Ⅱ）若该批产品共20件，从中任意抽取2件，X表示取出的2件产品中二等品的件数，求X的分布列与期望．

（本小题满分13分）某销售公司对其员工进行年终考核，在本次考核中只有合格和优秀两个等次，若考核为合格，则奖励奖金1万元；考核为优秀，奖励奖金2万元，假设甲、乙、丙三个分店考核为优秀的概率分别为、、，他们考核所得的等次相互独立．
（Ⅰ）求在这次考核中，甲、乙、丙三个员工中至少有一名考核为优秀的概率；
（Ⅱ）记在这次考核中甲、乙、丙三个员工所得的奖金之和为随机变量，求随机变量的分布列和数学期望。

第十一届西博会于2010年10月22日至26日在蓉举行，本届西博会以“绿色改变生活，技术引领发展”为主题。如此重要的国际盛会，自然少不了志愿者这支重要力量，“志愿者，西博会最亮丽的风景线”，通过他们的努力和付出，已把志愿者服务精神的种子播撒到人们心中。某大学对参加了本次西博会的该校志愿者实施“社会教育实践”学分考核，因该批志愿者表现良好，该大学决定考核只有合格和优秀两个等次，若某志愿者考核为合格，授予0.5个学分；考核为优秀，授予1个学分。假设该校志愿者甲、乙、丙考核为优秀的概率分别为、、，他们考核所得的等次相互独立。
（I）求在这次考核中，志愿者甲、乙、两三人中至少有一名考核为优秀的概率；
（II）求在这次考核中甲、乙、丙三名志愿者所得学分之和为整数的概率。

观察下面一组组合数等式：
；
；
；
…………
（1）由以上规律，请写出第个等式并证明；
（2）随机变量，求证：.

：某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响. 已知学生小张只选甲的概率为，只选修甲和乙的概率是，至少选修一门的概率是，用表示小张选修的课程门数和没有选修的课程门数的乘积.
（Ⅰ）求学生小张选修甲的概率；
（Ⅱ）记“函数 为上的偶函数”为事件，求事件的概率；
（Ⅲ）求的分布列和数学期望。           

（本小题满分12分）某牛奶厂要将一批牛奶用汽车从所在城市甲运至城市乙，已知从城市甲到城市乙只有两条公路，且运费由厂商承担．若厂商恰能在约定日期（×月×日）将牛奶送到，则城市乙的销售商一次性支付给牛奶厂20万元；若在约定日期前送到，每提前一天销售商将多支付给牛奶厂1万元；若在约定日期后送到，每迟到一天销售商将少支付给牛奶厂1万元．为保证牛奶新鲜度，汽车只能在约定日期的前两天出发，且只能选择其中的一条公路运送牛奶，已知下表内的信息：

统计信息 行驶路线	在不堵车的情况下到达城市乙所需时间（天）	在堵车的情况下到达城市乙所需时间（天）	堵车的概率	运费（万元）
公路1	2	3		1．6
公路2	1	4		0．8

（1）记汽车选择公路1运送牛奶时牛奶厂获得的毛收入为（单位：万元），求的分布列和数学期望；
（2）如果你是牛奶厂的决策者，你选择哪条公路运送牛奶有可能让牛奶厂获得的毛收入更多？
（注：毛收入＝销售商支付给牛奶厂的费用－运费）

以下茎叶图记录了甲、乙两组各四名同学的植树棵数．乙组记录中有一个数据模糊，无法确认，在图中以X表示．

(1)如果X＝8，求乙组同学植树棵数的平均数和方差；
(2)如果X＝9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数Y的分布列和数学期望．(注：方差s²＝ [(x₁－)²＋(x₂－)²＋…＋(x_n－)²]，其中为x₁，x₂，…，x_n的平均数)

（本小题满分10分）某研究性学习小组对某花卉种子的发芽率与昼夜温差之间的关系进行研究.他们分别记录了3月1日至3月5日的昼夜温差及每天30颗种子的发芽数，并得到如下资料：

日期	3月1日	3月2日	3月3日	3月4日	3月5日
温差x （度）	10	11	13	12	9
发芽数y（颗）	15	16	17	14	13

 
参考数据 ，其中
（1）请根据3月1日至3月5日的数据，求出y关于x的线性回归方程.据气象预报3月6日的昼夜温差为11℃，请预测3月6日浸泡的30颗种子的发芽数.（结果保留整数）
（2）从3月1日至3月5日中任选两天，记种子发芽数超过15颗的天数为X，求X的概率分布列，并求其数学期望和方差.

某高等学校自愿献血的50位学生的血型分布的情况如下表： 

血型	A	B	AB	O
人数	20	10	5	15

(1) 从这50位学生中随机选出2人，求这2人血型都为A型的概率；
（2）现有一位血型为A型的病人需要输血，要从血型为A，O的学生中随机选出2人准备献血，记选出A型血的人数为求随机变量的分布列及数学期望．

（本小题满分12分）根据以往的经验，某工程施工期间的降水量X（单位：mm）对工期的影响如下表：

降水量X	X<300	300≤X<700	700≤X<900	X≥900
工期延
误天数Y	0	2	6	10

 
历年气象资料表明，该工程施工期间降水量X小于300,700,900的概率分别为0．3 ,0．7 ,0．9．求：
（Ⅰ）工期延误天数Y的均值与方差；
（Ⅱ）在降水量X至少是300的条件下，工期延误不超过6天的概率．