高中数学随机思想的发展解答题

（本小题满分12分）近年来空气污染是一个生活中重要的话题， PM2．5就是其中一个指标。PM2．5指大气中直径小于或等于2．5微米的颗粒物，也称为可入肺颗粒物．PM2．5日均值在35微克／立方米以下空气质量为一级：在35微克／立方米～75微克／立方米之间空气质量为二级；在75微克／立方米以上空气质量为超标．淮北相山区2014年12月1日至I0日每天的PM2．5监测数据如茎叶图所示．

（1）期间的某天小刘来此地旅游，求当天PM2．5日均监测数据未超标的概率；
（2）陶先生在此期间也有两天经过此地，这两天此地PM2．5监测数据均未超标．请计算出这两天空气质量恰好有一天为一级的概率；
（3）从所给10天的数据中任意抽取三天数据，记表示抽到PM2．5监测数据超标的天数，求的分布列及期望．

某区要进行中学生篮球对抗赛，为争夺最后一个小组赛名额，甲、乙、丙三支篮球队要进行比赛，根据规则：每两支队伍之间都要比赛一场；每场比赛胜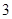者得分，负者得分，没有平局，获得第一名的将夺得这个参赛名额．已知乙队胜丙队的概率为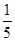，甲队获得第一名的概率为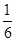，乙队获得第一名的概率为．
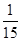（Ⅰ）求甲队分别战胜乙队和丙队的概率；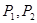
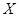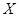（Ⅱ）设在该次比赛中，甲队得分为，求的分布列及期望．

（本小题满分12分）某旅行社组织了一个有36名游客的旅游团到安徽风景名胜地旅游，其中是省外游客，其余是省内游客，在省外游客中有玩过黄山，在省内游客中有玩过黄山。
（1）在该团中随机采访3名游客，求恰有1名 省外游客玩过黄山且省内游客玩过黄山少于2人的概率；
（2）在该团的省内游客中随机采访3名游客，设其中省内游客玩过黄山的人数为随机变量，求的分布列及数学期望

（本小题满分12分）甲、乙、丙三人射击同一目标，各射击一次，已知甲击中目标的概率为，乙与丙击中目标的概率分别为，每人是否击中目标是相互独立的．记目标被击中的次数为，且的分布列如下表：

（Ⅰ）求的值；
（Ⅱ）求的数学期望．

某校举行中学生“日常生活小常识”知识比赛,比赛分为初赛和复赛两部分，初赛采用选手从备选题中选一题答一题的方式进行；每位选手最多有5次答题机会，选手累计答对3题或答错3题即终止比赛，答对3题者直接进入复赛，答错3题者则被淘汰.已知选手甲答对每个题的概率均为，且相互间没有影响.
(1）求选手甲进入复赛的概率；
(2)设选手甲在初赛中答题的个数为，试求的分布列和数学期望.

生产A，B两种元件，其质量按测试指标划分为：指标大于或等于82为正品，小于82为次品，现随机抽取这两种元件各100件进行检测，检测结果统计如下：

测试指标	[70,76)	[76,82)	[82,88)	[88,94)	[94,100]
元件A	8	12	40	32	8
元件B	7	18	40	29	6

（1）试分别估计元件A、元件B为正品的概率；
（2）生产一件元件A，若是正品可盈利50元，若是次品则亏损10元；生产一件元件B，若是正品可盈利100元，若是次品则亏损20元，在（1）的前提下：
（i）求生产5件元件B所获得的利润不少于300元的概率；
（ii）记X为生产1件元件A和1件元件B所得的总利润，求随机变量X的分布列和数学期望．

某中学举行了一次“环保知识竞赛”活动．为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计．按照的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在的数据）．

（Ⅰ）求样本容量n和频率分布直方图中x、y的值；
（Ⅱ）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动，设表示所抽取的3名同学中得分在的学生个数，求的分布列及其数学期望．

A、B两个投资项目的利润率分别为随机变量X₁和X₂，根据市场分析，X₁和X₂的分布列分别为

X1	5%	10%
P	0.8	0.2

 

X2	2%	8%	12%
P	0.2	0.5	0.3

(1)在A，B两个项目上各投资100万元，Y₁和Y₂分别表示投资项目A和B所获得的利润，求方差V(Y₁)、V(Y₂)；
(2)将x(0≤x≤100)万元投资A项目，100－x万元投资B项目，f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和．求f(x)的最小值，并指出x为何值时，f(x)取到最小值．

甲、乙两名射手各打了10发子弹，其中甲击中环数与次数如下表

环数	5	6	7	8	9	10
次数	1	1	1	1	2	4

乙射击的概率分布列如表

环数	7	8	9	10
概率	0.2	0.3	p	0.1

(1)若甲，乙两人各打一枪，求共击中18环的概率及p的值；
(2)比较甲，乙两人射击水平的优劣．

为了促进学生的全面发展，某市教育局要求本市所有学校重视社团文化建设，2014年该市某中学的某新生想通过考核选拨进入该校的“电影社”和“心理社”，已知该同学通过考核选拨进入这两个社团成功与否相互独立．根据报名情况和他本人的才艺能力，两个社团都能进入的概率为，至少进入一个社团的概率为，并且进入“电影社”的概率小于进入“心理社”的概率.
（Ⅰ）求该同学分别通过选拨进入“电影社”的概率和进入“心理社”的概率；
（Ⅱ）学校根据这两个社团的活动安排情况，对进入“电影社”的同学增加1个校本选修课学分，对进入“心理社”的同学增加0.5个校本选修课学分．求该同学在社团方面获得校本选修课学分分数的分布列和数学期望.

（本小题满分12分）某校高一年级有四个班，其中一、二班为数学课改班，三、四班为数学非课改班．在期末考试中，课改班与非课改班的数学成绩优秀与非优秀人数统计如下表．

	优秀	非优秀	总计
课改班		50
非课改班	20		110
合计			210

 
（1）请完成上面的2´2列联表，并判断若按99%的可靠性要求，能否认为“成绩与课改
有关”；
（2）把全部210人进行编号，从编号中有放回抽取4次，每次抽取1个，记被抽取的4
人中的优秀人数为x，若每次抽取的结果是相互独立的，求x的分布列及数学期望Ex．

甲、乙两人各进行3次射击，甲每次击中目标的概率为，乙每次击中目标的概率为.
(1)求乙至多击中目标2次的概率；
(2)记甲击中目标的次数为Z，求Z的分布列、数学期望和标准差．

某地位于甲、乙两条河流的交汇处，根据统计资料预测，今年汛期甲河流发生洪水的概率为0.25，乙河流发生洪水的概率为0.18(假设两河流发生洪水与否互不影响)．现有一台大型设备正在该地工作，为了保护设备，施工部门提出以下三种方案：
方案1：运走设备，此时需花费4000元；
方案2：建一保护围墙，需花费1000元，但围墙只能抵御一个河流发生的洪水，当两河流同时发生洪水时，设备仍将受损，损失约56000元；
方案3：不采取措施，此时，当两河流都发生洪水时损失达60000元，只有一条河流发生洪水时，损失为10000元．
(1)试求方案3中损失费X(随机变量)的分布列；
(2)试比较哪一种方案好．

张华同学上学途中必须经过四个交通岗，其中在岗遇到红灯的概率均为，在岗遇到红灯的概率均为．假设他在4个交通岗遇到红灯的事件是相互独立的，X表示他遇到红灯的次数．
（1）若，就会迟到，求张华不迟到的概率；
（2）求EX．

第16届亚运会于2010年11月12日在广州举办，运动会期间来自广州大学和中山大学的共计6名大学生志愿者将被随机平均分配到跳水、篮球、体操这三个比赛场馆服务，且跳水场馆至少有一名广州大学志愿者的概率是.
(1)求6名志愿者中来自广州大学、中山大学的各有几人？
(2)设随机变量X为在体操比赛场馆服务的广州大学志愿者的人数，求X的分布列及均值．