对于函数 (a>0),如果方程
(a>0),如果方程 有相异两根
有相异两根 ,
, .
.
(1)若 ,且
,且 的图象关于直线x=m对称.求证:
的图象关于直线x=m对称.求证: ;
;
(2)若 且
且 ,求b的取值范围;
,求b的取值范围;
(3) 、
、 为区间
为区间 ,
, 上的两个不同的点,求证:
上的两个不同的点,求证: .
.
已知函数f(x)=ax2+bx+c,其中a∈N*,b∈N,c∈Z。
(1)若b>2a,且f(sinx)(x∈R)的最大值为2,最小值为-4,试求函数f(x)的最小值;
(2)若对任意实数x,不等式4x≤f(x)≤2(x2+1)恒成立,且存在x0,使得f(x0)<2(x02+1)成立,求c的值。
已知函数f(x)= ,其中
,其中
(I)若b>2a,且 f(sinx)(x∈R)的最大值为2,最小值为-4,试求函数f(x)的最小值;
(II)若对任意实数x,不等式 恒成立,且存在
恒成立,且存在 成立,求c的值。
成立,求c的值。
二次函数f(x)=
(I)若方程f(x)=0无实数根,求证:b>0;
(II)若方程f(x)=0有两实数根,且两实根是相邻的两个整数,求证:f(-a)= ;
;
(III)若方程f(x)=0有两个非整数实根,且这两实数根在相邻两整数之间,试证明存在整数k,使得 .
.
已知a>0,函数f(x)=ax-bx2,
(1)当b>0时,若对任意x∈R都有f(x)≤1,证明:a≤2 ;
;
(2)当b>1时,证明:对任意x∈[0, 1], |f(x)|≤1的充要条件是:b-1≤a≤2 ;
;
(3)当0<b≤1时,讨论:对任意x∈[0, 1], |f(x)|≤1的充要条件。
已知二次函数f(x)=ax2+bx+c和一次函数g(x)=-bx,其中a、b、c满足a>b>c,a+b+c=0,(a,b,c∈R).
(1)求证:两函数的图象交于不同的两点A、B;
(2)求线段AB在x轴上的射影A1B1的长的取值范围.
已知函数 的图像与
的图像与 轴正半轴的交点为
轴正半轴的交点为 ,
, =1,2,3,….
=1,2,3,….
求数列 的通项公式;
的通项公式;
令 为正整数), 问是否存在非零整数
为正整数), 问是否存在非零整数 , 使得对任意正整数
, 使得对任意正整数 ,都有
,都有 ? 若存在, 求出
? 若存在, 求出 的值 , 若不存在 , 请说明理由.
的值 , 若不存在 , 请说明理由.
已知函数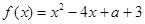 ,
,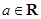 .
.
(Ⅰ)若函数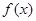 在
在 上至少有一个零点,求
上至少有一个零点,求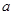 的取值范围;
的取值范围;
(Ⅱ)若函数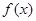 在
在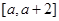 上的最大值为
上的最大值为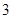 ,求
,求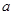 的值.
的值.
试题篮
()