(本小题满分12分)
已知函数f(x)=x2-ax+b (a,b∈R)的图像经过坐标原点,且 ,数列{
,数列{ }的前n项和
}的前n项和 =f(n)(n∈N*).
=f(n)(n∈N*).
(Ⅰ) 求数列{ }的通项公式;(Ⅱ)若数列{
}的通项公式;(Ⅱ)若数列{ }满足
}满足 +
+ =
=  ,求数列{
,求数列{ }的前n项和.
}的前n项和.
(本小题满分12分)
对于定义在区间D上的函数 ,若存在闭区间
,若存在闭区间 和常数
和常数 ,使得对任意
,使得对任意 ,都有
,都有 ,
,
且对任意 ∈D,当
∈D,当 时,
时, 恒成立,则称函数
恒成立,则称函数 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.
(Ⅰ)判断函数 和
和 是否为R上的“平底型”函数?并说明理由;
是否为R上的“平底型”函数?并说明理由;
、已知 且
且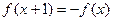 ,则
,则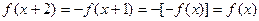 ,得
,得 的一个周期为2,类比上述结论,请写出下列两个函数的一个周期.
的一个周期为2,类比上述结论,请写出下列两个函数的一个周期.
(1)已知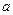 为正的常数,
为正的常数, 且
且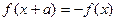 ,求
,求 的一个周期;
的一个周期;
(2)已知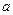 为正的常数,
为正的常数, 且
且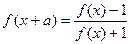 ,求
,求 的一个周期.
的一个周期.
(本小题满分15分)
设函数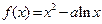 与
与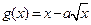 的图像分别交直线
的图像分别交直线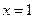 于点
于点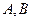 ,且曲线
,且曲线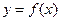 在点
在点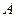 处的切线与曲线
处的切线与曲线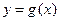 在点
在点 处的切线平行.
处的切线平行.
(1)求函数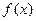 ,
, 的表达式;
的表达式;
(2)设函数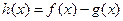 ,求函数
,求函数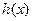 的最小值;
的最小值;
(3)若不等式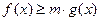 在
在 上恒成立,求实数
上恒成立,求实数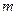 的取值范围.
的取值范围.
已知函数f(x)=x|x2-3|,x∈[0,m]其中m∈R,且m>0.
(1)若m<1,求证:函数f(x)是增函数。
(2)如果函数f(x)的值域是[0,2],试求m的取值范围。
(3)如果函数f(x)的值域是[0,λm2],试求实数λ的最小值
(本小题满分13分)
古汉集团生产的A,B两种型号的口服液供出口,国家为鼓励产品出口,采用出口退税政策:出 口价值为a万元的/1产品可获得
口价值为a万元的/1产品可获得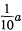 万元的退税款,出口价值为b万元的B产品可获得
万元的退税款,出口价值为b万元的B产品可获得 万元的退税款.已知厂家出口总价值为100万元的A、B两种口服液,且两种口服液的出口价值都不低于10万元.
万元的退税款.已知厂家出口总价值为100万元的A、B两种口服液,且两种口服液的出口价值都不低于10万元.
(1) 当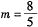 时,请你制定一个方案,使得在这次出口贸易中该企业获得的退税款最多,并求出其最大值;(精确到0.1,参考数据:
时,请你制定一个方案,使得在这次出口贸易中该企业获得的退税款最多,并求出其最大值;(精确到0.1,参考数据: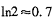 )
)
(2) 记该企业获得的退税款的最大值函数为,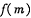 ,求
,求 的表达式.
的表达式.
已知函数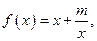 且此函数图象过点(1,5).(1)求实数m的值; (2)判断f(x)奇偶性;(3)讨论函数f(x)在
且此函数图象过点(1,5).(1)求实数m的值; (2)判断f(x)奇偶性;(3)讨论函数f(x)在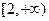 上的单调性?并证明你的结论.
上的单调性?并证明你的结论.
(本小题满分12分)
在股票市场上 ,投资者常参考股价(每一股的价格)的某条平滑均线(记作MA)的变化情况来决定买入或卖出股票。股民老王在研究股票的走势图时,发现一只股票的MA均线近
,投资者常参考股价(每一股的价格)的某条平滑均线(记作MA)的变化情况来决定买入或卖出股票。股民老王在研究股票的走势图时,发现一只股票的MA均线近 期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解
期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解 析式
析式 来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线
来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线 对称。老王预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线
对称。老王预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线 对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F。
对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F。
现在老王决定取点 ,点
,点 ,点
,点 来确定解析式中的常数
来确定解析式中的常数 ,并且已经求得
,并且已经求得 。
。
(1)请你帮老王算出 ,并回答股价什么时候见顶(即求F点的横坐标);
,并回答股价什么时候见顶(即求F点的横坐标);
(2)老王如能在今天以D点处的价格买入该股票5000股,到见顶处F点的价格全部卖出,不计其它费用,这次操作他能赚多少元?
(本小题满分14分)
已知集合 是满足下列性质的函数
是满足下列性质的函数 的全体:在定义域内存在
的全体:在定义域内存在 ,使得
,使得 成立。
成立。
(Ⅰ)函数 是否属于集合
是否属于集合 ?说明理由;
?说明理由;
(Ⅱ)设函数 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)设函数 图象与函数
图象与函数 的图象有交点,证明:函数
的图象有交点,证明:函数 .
.
(本小题满分14分)
建造一容积为8 深为2m的长方体形无盖水池,每
深为2m的长方体形无盖水池,每 池底和池壁造价各为120元和80元.
池底和池壁造价各为120元和80元.
(1)求总造价关于一边长x的函数解析式,并指出该函数的定义域;
(2)判断(1)中函数在 和
和 上的单调性;
上的单调性;
(3)如何设计水池尺寸,才能使总造价最低;
试题篮
()