高中数学三面角、直三面角的基本性质解答题

（本小题共12分）
已知函数f(x)＝2x－－aln(x＋1)，a∈R．（1）若a＝－4，求函数f(x)的单调区间；
（2）求y＝f(x)的极值点（即函数取到极值时点的横坐标）．

已知函数，且定义域为（0，2）.
(1）求关于x的方程+3在（0，2）上的解；
（2）若是定义域(0，2)上的单调函数，求实数的取值范围；
（3）若关于x的方程在（0，2）上有两个不同的解，求k的取值范围。

已知二次函数（其中）
（1）试讨论函数的奇偶性.
（2）当为偶函数时，若函数，
试证明：函数在上单调递减，在上单调递增；

知，，
（1）求的值.
（2）x_1、x_2、…x₂₀₁₀均为正实数，若函数f(x)＝log_ax(a＞0且a≠1)且f(x₁x₂…x₂₀₁₀)＝，
求f()＋f()＋…＋f()的值

已知是定义在[-1,1]上的奇函数，且，若任意的，当时，总有．
（1）、判断函数在[-1,1]上的单调性，并证明你的结论；   
（2）、解不等式：；
（3）、若对所有的恒成立，其中（是常数），求实数的取值范围．

已知函数（且）
（1）若函数在上的最大值与最小值的和为2，求的值；
（2）将函数图象上所有的点向左平移2个单位长度，再向下平移1个单位长度，得到函数的图象，写函数的解析式；
（3）若（2）中平移后所得的函数的图象不经过第二象限，求的取值范围.

已知定义在R上的函数，其中a、b为常数。
（1）若曲线在点处的切线方程为，求a、b的值；
（2）若，且函数在处取得最大值，求实数a的取值范围。

已知函数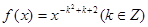满足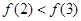
（1）求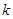的值并求出相应的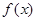的解析式
（2）对于（1）中得到的函数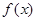，试判断是否存在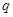，使得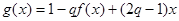 
在[－1， 2]上值域为[－4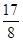，]？若存在，求出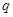；若不存在，请说明理由.

已知函数（其中）.
（Ⅰ）求的单调区间；
（Ⅱ）求在上的最大值与最小值.

设函数，曲线在点处的切线方程为
，求的解析式.

某品牌电视生产厂家有A、B两种型号的电视机参加了家电下乡活动，若厂家A、B对两种型号的电视机的投放金额分别为p、q万元，农民购买电视机获得的补贴分别为p、lnq万元，已知A、B两种型号的电视机的投放总额为10万元，且A、B两种型号的电视机的投放金额均不低于1万元，请你制定一个投放方案，使得在这次活动中农民得到的补贴最多，并求出最大值(精确到0.1，参考数据：)．

某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算，如果将楼房建为x(≥10)层，则每平方米的平均建筑费用为560+48（单位：元）.为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？
（注：平均综合费用＝平均建筑费用+平均购地费用，平均购地费用＝）

某商品在近30天内每件的销售价格p（元）与时间t（天）的函数关系是该商品的日销售量Q（件）与时间t（天）的函数关系是，求这种商品的日销售金额的最大值，并指出日销售金额最大的一天是30天中的第几天？

对于二次函数，
（1）指出图像的开口方向、对称轴方程、顶点坐标；
（2）画出它的图像，并说明其图像由的图像经过怎样平移得来；
（3）求函数的最大值或最小值；
（4）分析函数的单调性。

证明：函数是偶函数，且在上是增加的。