(本小题满分16分)
某厂生产一种仪器,由于受生产能力和技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率 与日产量
与日产量 (件)之间大体满足关系:
(件)之间大体满足关系:
(注:次品率 ,如
,如 表示每生产10件产品,约有1件为次品.其余为合格品.)
表示每生产10件产品,约有1件为次品.其余为合格品.)
已知每生产一件合格的仪器可以盈利 元,但每生产一件次品将亏损
元,但每生产一件次品将亏损 元,故厂方希望定出合适的日产量,
元,故厂方希望定出合适的日产量,
(1)试将生产这种仪器每天的盈利额 (元)表示为日产量
(元)表示为日产量 (件)的函数;
(件)的函数;
(2)当日产量 为多少时,可获得最大利润?
为多少时,可获得最大利润?
(满分10分)某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品还需再向总公司交 元(
元( )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为 元(
元( )时,一年的销售量为
)时,一年的销售量为 万件.
万件.
(1)求分公司一年的利润 (万元)与每件产品的售价
(万元)与每件产品的售价 的函数关系式;
的函数关系式;
(2)当每件产品的售价为多少元时,分公司一年的利润 最大,
最大,
并求出 的最大值
的最大值
(本小题满分12分)
设函数f(x)= +
+ -1.
-1.
(1)若x≥0时,f(x)≥0恒成立,求a的取值范围;
(2)求证:对于大于1的正整数n,恒有1+ <
< <1+
<1+ 成立.
成立.
(12分)设函数 满足条件f(-1+x)=f(-1-x),且关于x的不等式
满足条件f(-1+x)=f(-1-x),且关于x的不等式 的解集为
的解集为
(1)求函数f(x)的解析式;
(2)若 时,不等式
时,不等式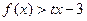 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。
某高速公路某施工工地需调运建材100吨,可租用装载的卡车和农用车分别为10辆和20辆,若每辆卡车装载8吨,运费960元,每辆农用车装载2.5吨,运费360元,问两种车各租用多少辆时,才能一次性装完且总费用最低?
某化工企业2007年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以 后每年的维护费都比上一年增加2万元.
后每年的维护费都比上一年增加2万元.
(1)求该企业使用该设备 年的年平均污水处理费用
年的年平均污水处理费用 (万元);
(万元);
(2)问为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水
某市旅游部门开发一种旅游纪念品,每件产品的成本是 元,销售价是
元,销售价是 元,月平均销售
元,月平均销售 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是 (元).
(元).
(Ⅰ)写出 与
与 的函数关系式;
的函数关系式;
(Ⅱ)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大
、统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为: 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(Ⅰ)当汽车以40千米/小时的速度匀 速行驶时,从甲地到乙地要耗油多少升?
速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多 大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
四、附加题:(本大题共1小题,共15分.解答应写出文字说明,证明过程或演算步骤.)
23.(本小题满分15分)
已知函数 .
.
(Ⅰ)求函数 的最大值;
的最大值;
(Ⅱ)当 时,求证
时,求证 .
.
已知函数 ,点
,点 .
.
(Ⅰ)若 ,函数
,函数 在
在 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求 的取值范围;
的取值范围;
(Ⅱ) 当 时,
时, 对任意的
对任意的 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(Ⅲ)若 ,函数
,函数 在
在 和
和 处取得极值,且
处取得极值,且 ,
, 是坐标原点,证明:直线
是坐标原点,证明:直线 与直线
与直线 不可能垂直.
不可能垂直.
(本小题满分12分)
某公园准备建一个摩天轮,摩天轮的外围是一个周长为 米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为
米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为 元/根,且当两相邻的座位之间的圆弧长为
元/根,且当两相邻的座位之间的圆弧长为 米时,相邻两座位之间的钢管和其中一个座位的总费用为
米时,相邻两座位之间的钢管和其中一个座位的总费用为 元,假设座位等距离分布,且至少有四个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为
元,假设座位等距离分布,且至少有四个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为 元.
元.
(Ⅰ)试写出 关于
关于 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(Ⅱ)当 米时,试确定座位的个数,使得总造价最
米时,试确定座位的个数,使得总造价最 低?
低?
试题篮
()