((本小题满分14分)
已知函数 满足
满足 当
当 ,当
,当 的最大值为
的最大值为 。
。
(1)求 时函数
时函数 的解析式;
的解析式;
(2)是否存在实数 使得不等式
使得不等式 对于
对于 若存在,求出实数
若存在,求出实数  的取值集合,若不存在,说明理由.
的取值集合,若不存在,说明理由.
已知函数f(x)是定义在R上的偶函数,当x
 0时,f(x)=
0时,f(x)= .
.
(1)画出函数f(x)的图象.
(2)根据图象写出 f(x)的单调区间,并写出函数的值域。
f(x)的单调区间,并写出函数的值域。
(本题满分10分)
如图,要计算西湖岸边两景点 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和 两点,现测得
两点,现测得 ,
, ,
, ,
, ,
, ,求两景点
,求两景点 与
与 的距离(精确到0.1km).参考数据:
的距离(精确到0.1km).参考数据:
.(本题满分12分)
已知函数f(x)=(a,b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(1)求f(x)的解析式;
(2)设k>1,解关于x的不等式f(x)<.
. (满分12分 )定义在
)定义在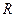 上的函数
上的函数 满足
满足 ,且
,且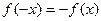
 ,当
,当 时,
时,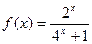 。1)求
。1)求 在
在 上的解析式;
上的解析式;
2)若 在
在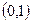 上是减函数,求函数
上是减函数,求函数 在
在 上的值域。
上的值域。
(本小题满分14分)
已知定义域为 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件:
① 对任意的 ,总有
,总有 ≥0; ②
≥0; ② ;
;
③若 且
且 ,则有
,则有 成立,并且称
成立,并且称 为“友谊函数”,
为“友谊函数”,
请解答下列各题:
(1)若已知 为“友谊函数”,求
为“友谊函数”,求 的值;
的值;
(2)函数 在区间
在区间 上是否为“友谊函数”?并给出理由.
上是否为“友谊函数”?并给出理由.
(3)已知 为“友谊函数”,且
为“友谊函数”,且  ,求证:
,求证:
为赢得2010年广州亚运会的商机,某商家最近进行了新科技产品的市场分析,调查显示,新产品每件成本9万元,售价为30万元,每星期卖出432件,如果降低价格,销售 量可以增加,且每星期多卖出的商品件数与商品单价的降低值
量可以增加,且每星期多卖出的商品件数与商品单价的降低值 (单位:万元,
(单位:万元, )的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.(1)将一个星期的商品销售利润表示成
)的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.(1)将一个星期的商品销售利润表示成 的函数;
的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
(本小题满分12分)
某房地产开发商投资8 1万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元.
1万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元.
(Ⅰ)若扣除投资和各种装修费,则从第几年开始获取纯利润?
(Ⅱ)若干年后开 发商为了投资其他项目,有两种处理方案:①年平均利润最大时以46万元出售该楼; ②纯利润总和最大时,以10万元出售该楼,问哪种方案盈利更多?
发商为了投资其他项目,有两种处理方案:①年平均利润最大时以46万元出售该楼; ②纯利润总和最大时,以10万元出售该楼,问哪种方案盈利更多?
(本小题满分13分)
已知定义域为R的函数 是奇函数.
是奇函数.
(1)求a的值;(2)判断 的单调性(不需要写出理由);
的单调性(不需要写出理由);
(3)若对任意的 ,不等式
,不等式 恒成立,求
恒成立,求 的取
的取 值范
值范 围.
围.
(本小题满分12分)
已知函数f(x)=x2-ax+b (a,b∈R)的图像经过坐标原点,且 ,数列{
,数列{ }的前n项和
}的前n项和 =f(n)(n∈N*).
=f(n)(n∈N*).
(Ⅰ) 求数列{ }的通项公式;(Ⅱ)若数列{
}的通项公式;(Ⅱ)若数列{ }满足
}满足 +
+ =
=  ,求数列{
,求数列{ }的前n项和.
}的前n项和.
(本小题满分14分)
已知实系数一元二次方程x2+px+q=0的两根分别为x1,x2。
(1)若上述方程的一个根x1=4-i(i为虚数单位),求实数p,q的值;
(2)若方程的两根满足|x1|+|x2|=2,求实数p的取值范围。
试题篮
()