(本小题满分8分)
某交易市场的土豆在30天内每吨的交易价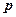 (千元)与时间
(千元)与时间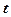 (天)(
(天)(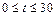 ),组成有序数对
),组成有序数对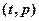 ,点
,点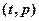 落在如图所示的两条线段上,该市场土豆在30天内的日交易量
落在如图所示的两条线段上,该市场土豆在30天内的日交易量 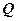 (吨)与时间
(吨)与时间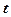 (天)的部分数据如下表所示
(天)的部分数据如下表所示
第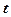 天 天 |
4 |
10 |
16 |
22 |
 (吨) (吨) |
36 |
30 |
24 |
18 |
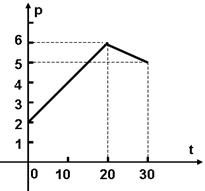
(1)根据提供的图象,写出每吨交易价格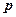 (千元)与时间
(千元)与时间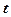 (天)所满足函数关系式;
(天)所满足函数关系式;
(2)根据表中数据确定日交易量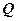 (吨)与时间
(吨)与时间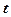 (天)的一次函数解析式;
(天)的一次函数解析式;
(3)用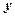 表示日交易额(千元),写出
表示日交易额(千元),写出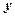 关于
关于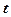 的函数解析式,问这30天中第几天交易额最大,最大值多少?
的函数解析式,问这30天中第几天交易额最大,最大值多少?
已知函数
 (
( 是常数),且
是常数),且 ,
, .
.
(1) 求 的值;
的值;
(2) 当 时,判断
时,判断 的单调性
的单调性 并证明;
并证明;
(3) 对任意的 ,若不等式
,若不等式

 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)
在股票市场上 ,投资者常参考股价(每一股的价格)的某条平滑均线(记作MA)的变化情况来决定买入或卖出股票。股民老王在研究股票的走势图时,发现一只股票的MA均线近
,投资者常参考股价(每一股的价格)的某条平滑均线(记作MA)的变化情况来决定买入或卖出股票。股民老王在研究股票的走势图时,发现一只股票的MA均线近 期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解
期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解 析式
析式 来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线
来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线 对称。老王预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线
对称。老王预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线 对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F。
对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F。
现在老王决定取点 ,点
,点 ,点
,点 来确定解析式中的常数
来确定解析式中的常数 ,并且已经求得
,并且已经求得 。
。
(1)请你帮老王算出 ,并回答股价什么时候见顶(即求F点的横坐标);
,并回答股价什么时候见顶(即求F点的横坐标);
(2)老王如能在今天以D点处的价格买入该股票5000股,到见顶处F点的价格全部卖出,不计其它费用,这次操作他能赚多少元?
(本小题满分14分)
已知集合 是满足下列性质的函数
是满足下列性质的函数 的全体:在定义域内存在
的全体:在定义域内存在 ,使得
,使得 成立。
成立。
(Ⅰ)函数 是否属于集合
是否属于集合 ?说明理由;
?说明理由;
(Ⅱ)设函数 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)设函数 图象与函数
图象与函数 的图象有交点,证明:函数
的图象有交点,证明:函数 .
.
(本小题满分14分)
建造一容积为8 深为2m的长方体形无盖水池,每
深为2m的长方体形无盖水池,每 池底和池壁造价各为120元和80元.
池底和池壁造价各为120元和80元.
(1)求总造价关于一边长x的函数解析式,并指出该函数的定义域;
(2)判断(1)中函数在 和
和 上的单调性;
上的单调性;
(3)如何设计水池尺寸,才能使总造价最低;
((本小题12分)
已知指数函数 满足:g(2)=4,定义域为
满足:g(2)=4,定义域为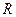 的函数
的函数 是奇函数。
是奇函数。
(1)确定 的解析式;
的解析式;
(2)求m,n的值;
(3)若对任意的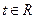 ,不等式
,不等式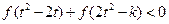 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
((本小题12分)
经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天) 的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20-
的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20- |t-10|.
|t-10|.
(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式;
(2)求该种商品的日销售额y的最大值与最小值.
.函数 (
( 为实常数).
为实常数).
(1)若 ,求
,求 的单调区间;
的单调区间;
(2)若 ,设
,设 在区间
在区间 的最小值为
的最小值为 ,求
,求 的表达式
的表达式
.(本小题满分12分)设函数 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意实数
,且对任意实数 ,都有
,都有 成立,数列
成立,数列 满足
满足 且
且
(1)求 的值;
的值;
(2)若不等式 对一切
对一切 均成立,求
均成立,求 的最大值.
的最大值.
试题篮
()