某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙,地面利用原地面均不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,屋顶每平方米造价20元.
(1)仓库面积 的最大允许值是多少?
的最大允许值是多少?
(2)为使面积 达到最大而实际投入又不超过预算,正面铁栅应设计为多长?
达到最大而实际投入又不超过预算,正面铁栅应设计为多长?
已知函数 ,g(x)=
,g(x)= ,a,b∈R.
,a,b∈R.
(1)求函数f(x)的单调区间;
(2)记函数h(x)=f(x)+g(x),当a=0时,h(x)在(0,1)上有且只有一个极值点,求实数b的取值范围;
(3)记函数F(x)=|f(x)|,证明:存在一条过原点的直线l与y=F(x)的图象有两个切点.
已知函数f(x)= (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式f(x)<  .
.
已知函数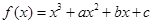 ,曲线
,曲线 在点
在点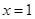 处的切线为
处的切线为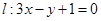 ,若
,若 时,
时, 有极值.
有极值.
(1)求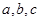 的值;
的值;
(2)求 在
在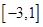 上的最大值和最小值.
上的最大值和最小值.
已知函数f(x)=|x+1|,g(x)=2|x|+a.
(1)当a=0时,解不等式f(x)≥g(x);
(2)若任意x∈R,f(x) g(x)恒成立,求实数a的取值范围.
g(x)恒成立,求实数a的取值范围.
设p:函数y=loga(x+1)(a>0且a≠1)在(0,+∞)上单调递减; q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p∧q为假,p∨q为真,求实数a的取值范围.
某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率P与日产量x(万件)之间大体满足关系: (其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
已知m∈R,对p:x1和x2是方程x2-ax-2=0的两个根,不等式|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立;q:函数f(x)=3x2+2mx+m+ 有两个不同的零点.求使“p且q”为假命题、“p或q”为真命题的实数m的取值范围.
有两个不同的零点.求使“p且q”为假命题、“p或q”为真命题的实数m的取值范围.
提高过江大桥的车辆通行能力可改善整个城市的交通状况。在一般情况下,大桥上的车流速度 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当
(单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当 时,车流速度
时,车流速度 是车流密度
是车流密度 的一次函数。
的一次函数。
当 时,求函数
时,求函数 的表达式;
的表达式;
当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时) 可以达到最大?并求出最大值。(精确到1辆/小时)
可以达到最大?并求出最大值。(精确到1辆/小时)
试题篮
()