(本小题满分10分)设有两个命题: 关于x的不等式x2+2ax+4>0对一切x∈R恒成立;
关于x的不等式x2+2ax+4>0对一切x∈R恒成立; 函数f(x)=-(4-2a)x在(-∞,+∞)上是减函数.若命题
函数f(x)=-(4-2a)x在(-∞,+∞)上是减函数.若命题 为真,
为真, 为假,则实数a的取值范围是多少?
为假,则实数a的取值范围是多少?
已知命题p:函数f(x)=x2+ax-2在[-1,1]内有且仅有一个零点.命题q:x2+3(a+1)x+2≤0在区间[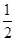 ,
, ]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.
]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.
已知命题 “存在
“存在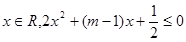 ”,命题
”,命题 :“曲线
:“曲线 表示焦点在
表示焦点在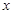 轴上的椭圆”,命题
轴上的椭圆”,命题 “曲线
“曲线 表示双曲线”
表示双曲线”
(1)若“ 且
且 ”是真命题,求
”是真命题,求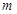 的取值范围;
的取值范围;
(2)若 是
是 的必要不充分条件,求
的必要不充分条件,求 的取值范围。
的取值范围。
下列说法:(1)命题“ ”的否定是“
”的否定是“ ”;
”;
(2)关于 的不等式
的不等式 恒成立,则
恒成立,则 的取值范围是
的取值范围是 ;
;
(3)对于函数 ,则有当
,则有当 时,
时, ,使得函数
,使得函数  在
在 上有三个零点;
上有三个零点;
(4)
(5)已知 ,且
,且 是常数,又
是常数,又 的最小值是
的最小值是 ,则
,则 7.其中正确的个数是 .
7.其中正确的个数是 .
(1)已知命题 和命题
和命题 ,若
,若 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
(2)已知命题 方程
方程 的一根在
的一根在 内,另一根在
内,另一根在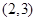 内.
内.
命题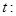 函数
函数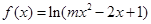 的定义域为全体实数.
的定义域为全体实数.
若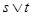 为真命题,求实数
为真命题,求实数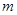 的取值范围.
的取值范围.
试题篮
()