给定两个命题,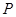 :对任意实数
:对任意实数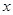 都有
都有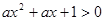 恒成立;
恒成立;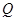 :关于
:关于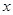 的方程
的方程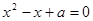 有实数根;如果“
有实数根;如果“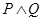 ”为假,且“
”为假,且“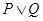 ”为真,求实数
”为真,求实数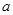 的取值范围。
的取值范围。
已知命题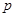 :
: 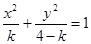 表示焦点在
表示焦点在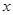 轴上的椭圆,命题
轴上的椭圆,命题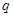 :
: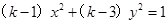 表示双曲线。若
表示双曲线。若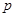 或
或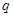 为真,
为真,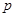 且
且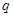 为假,求
为假,求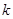 的取值范围。
的取值范围。
(本题满分16分) 本题共有3个小题,第1小题满分7分,第2小题满分7分,第3小题满分2分.
设直线 交椭圆
交椭圆 于
于 两点,交直线
两点,交直线 于点
于点 .
.
(1)若 为
为 的中点,求证:
的中点,求证: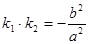 ;
;
(2)写出上述命题的逆命题并证明此逆命题为真;
(3)请你类比椭圆中(1)、(2)的结论,写出双曲线中类似性质的结论(不必证明).
已知函数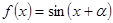 ,
, 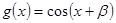 ,
,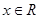 ,
,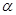 、
、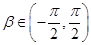 .
.
(Ⅰ)若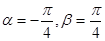 ,判断
,判断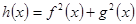 的奇偶性;
的奇偶性;
(Ⅱ) 若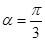 ,
,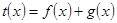 是偶函数,求
是偶函数,求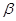 ;
;
(Ⅲ)是否存在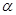 、
、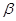 ,使得
,使得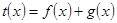 是奇函数但不是偶函数?若存在,试确定
是奇函数但不是偶函数?若存在,试确定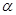 与
与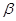 的关系式;如果不存在,请说明理由.
的关系式;如果不存在,请说明理由.
试题篮
()