一个半径为1的小球在一个内壁棱长为 的正四面体容器内可向各个方向自由运动,则该小球永远不可能接触到的容器内壁的面积是.
的正四面体容器内可向各个方向自由运动,则该小球永远不可能接触到的容器内壁的面积是.
一个六棱柱的底面是正六边形,其侧棱垂直于底面.已知该六棱柱的顶点都在同一球面上,且该六棱柱的体积为 98,底面周长为3,则这个球的体积为.
如图所示,在确定的四面体 中,截面
中,截面 平行于对棱
平行于对棱 和
和 .
.
(1)若 ⊥
⊥ ,则截面
,则截面 与侧面
与侧面 垂直;
垂直;
(2)当截面四边形 面积取得最大值时,
面积取得最大值时, 为
为 中点;
中点;
(3)截面四边形 的周长有最小值;
的周长有最小值;
(4)若 ⊥
⊥ ,
, ,则在四面体内存在一点
,则在四面体内存在一点 到四面体
到四面体 六条棱的中点的距离相等.上述说法正确的是.
六条棱的中点的距离相等.上述说法正确的是.
已知矩形 的周长为
的周长为 ,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为.
,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为.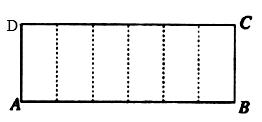
试题篮
()