高中数学表面展开图试题

一简单组合体的三视图如图所示，则该组合体的体积为（  ）

A．	B．
C．	D．

已知三棱柱的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为，，，则此球的表面积等于__________．

如图，在四棱锥中，，平面，平面，，，．

（Ⅰ）求棱锥的体积；
（Ⅱ）求证：平面平面；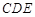
（Ⅲ）在线段上是否存在一点，使平面？若存在，求出的值；若不存在，说明理由．

一个几何体的三视图如图所示，则该几何体的体积为（  ）

A．

B．

C．

D．

表面积为的球面上有四点且是等边三角形，球心O到平面ABC的距
离为，若,则棱锥体积的最大值为          ．

已知某几何体的三视图如图所示，则该几何体的体积等于（  ）

A．	B．160
C．	D．60

如图所示，在四边形中，,将四边形沿对角线折成四面体，使平面平面，则下列结论正确的是          ．

（1）；
（2）；
（3）与平面所成的角为；   
（4）四面体的体积为．

已知三棱锥OABC,A,B,C三点均在球心为O的球表面上,AB=BC=1,∠ABC=120°,三棱锥OABC的体积为,则球O的表面积是(  )

A．

B．

C．

D．

一个三棱锥的正视图和俯视图如图所示，则它的侧视图的面积为（   ）

A．

B．

C．

D．

在如图所示的多面体ABCDE中，AB∥DE，AB⊥AD，△ACD是正三角形，AD=DE=2AB=2，，F是CD的中点．

（Ⅰ）求证AF∥平面BCE；
（Ⅱ）求多面体ABCDE的体积．

已知三棱锥,A,B,C三点均在球心为O的球表面上,AB=BC=1,∠ABC=120°,三棱锥的体积为,则球的表面积是（ ）

A．

B．

C．

D．

一个三棱锥的正视图和俯视图如图所示，则它的侧视图的面积为（   ）

A．

B．

C．

D．

若某几何体的三视图（单位：cm）如图所示，则该几何体的体积等于（   ）

A．

B．

C．

D．

已知四棱锥，其中，，面，，为的中点．

（1）求证：面；
（2）求证：面面；
（3）求四棱锥的体积．

如图，四棱锥中，底面为矩形，平面，为的中点．

（1）证明：平面；
（2）设二面角为60°，，求三棱锥的体积．