(本小题12分)已知函数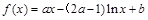 .
.
(Ⅰ)若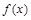 在点(
在点(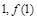 )处的切线方程为
)处的切线方程为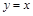 ,求实数
,求实数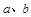 的值;
的值;
(Ⅱ)当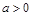 时,讨论
时,讨论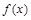 的单调性;
的单调性;
(Ⅲ)当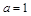 时,
时,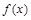 在区间
在区间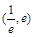 上恰有一个零点,求实数
上恰有一个零点,求实数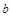 的取值范围.
的取值范围.
(本小题满分12分)已知函数f(x)=x2-2(a+1)x+2alnx(a>0).
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)的单调区间;
(3)若f(x)≤0在区间[1,e]上恒成立,求实数a的取值范围.
已知函数f(x)=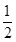 (x2+a)的图象在点Pn(n,f(n))(n∈N*)处的切线ln的斜率为kn,直线ln交x轴,y轴分别于点An(xn,0),Bn(0,yn),且y1=-1.给出以下结论:
(x2+a)的图象在点Pn(n,f(n))(n∈N*)处的切线ln的斜率为kn,直线ln交x轴,y轴分别于点An(xn,0),Bn(0,yn),且y1=-1.给出以下结论:
①a=-1;
②记函数g(n)=xn(n∈N*),则函数g(n)的单调性是先减后增,且最小值为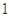 ;
;
③当n∈N*时,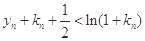 ;
;
④当n∈N*时,记数列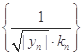 的前
的前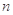 项和为
项和为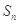 ,则
,则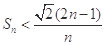 .
.
其中,正确的结论有 (写出所有正确结论的序号)
(本小题满分12分)已知函数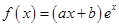 (
(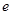 为自然对数的底数),曲线
为自然对数的底数),曲线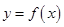 在点
在点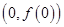 处的切线方程为
处的切线方程为 .
.
(1)求 ,
, 的值;
的值;
(2)任意 ,
, 时,证明:
时,证明: .
.
(本小题满分13分)已知函数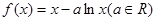 .
.
(1)当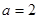 时,求曲线
时,求曲线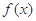 在
在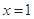 处的切线方程;
处的切线方程;
(2)设函数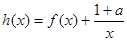 ,求函数
,求函数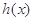 的单调区间;
的单调区间;
(3)若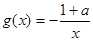 ,在
,在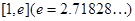 上存在一点
上存在一点 ,使得
,使得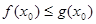 成立,求
成立,求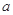 的取值范围.
的取值范围.
(本小题满分14分)设函数f(x)=(x–1)2+alnx,a∈R.
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线与直线x+2y–1=0垂直,求a的值;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)若函数f(x)有两个极值点x1,x2且x1<x2,求证:f(x2)>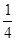 –
–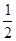 ln2.
ln2.
函数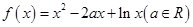 .
.
(I)函数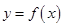 在点
在点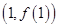 处的切线与直线
处的切线与直线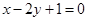 垂直,求a的值;
垂直,求a的值;
(II)讨论函数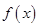 的单调性;
的单调性;
(III)不等式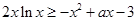 在区间
在区间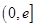 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
(本小题满分14分)设函数 ,
,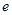 是自然对数的底数,
是自然对数的底数,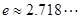 ,
,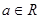 为常数.
为常数.
(1)若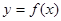 在
在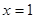 处的切线
处的切线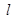 的斜率为
的斜率为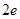 ,求
,求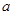 的值;
的值;
(2)在(1)的条件下,证明切线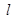 与曲线
与曲线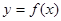 在区间
在区间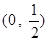 至少有1个公共点;
至少有1个公共点;
(3)若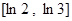 是
是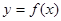 的一个单调区间,求
的一个单调区间,求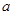 的取值范围.
的取值范围.
试题篮
()