高中数学组合几何试题

若存在实常数和，使得函数和对其定义域上的任意实数分别满足：和，则称直线为和的“隔离直线”.已知函数和函数，那么函数和函数的隔离直线方程为_________.

（本小题满分12分）已知函数f（x）＝x²－2（a＋1）x＋2alnx（a>0）．
（1）当a＝1时，求曲线y＝f（x）在点（1，f（1））处的切线方程；
（2）求f（x）的单调区间；
（3）若f（x）≤0在区间[1，e]上恒成立，求实数a的取值范围．

已知函数
(1)当a=2时，求曲线在点处的切线方程;
(2)求函数的极值.

已知函数（k为常数，e=2.71828…是自然对数的底数），曲线在点处的切线与x轴平行．
(1)求k的值及的单调区间;
(2)设其中为的导函数,证明:对任意,.

（1）已知函数,过点Ｐ的直线与曲线相切，求的方程；
（2）设，当时，在１,４上的最小值为，求在该区间上的最大值．

【原创】已知函数=（）．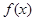
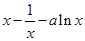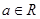（Ⅰ）当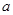=1时，求函数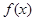在（1,0）点的切线方程；
（Ⅱ）当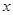＞1时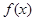，＞0,求实数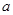的取值范围．

已知函数f（x）＝x（x＋a）－lnx，其中a为常数.
（1）求f（x）的单调区间；
（2）问过坐标原点可以作几条直线与曲线y＝f（x）相切？并说明理由；
（3）若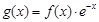在区间（0，1）内是单调函数，求a的取值范围.

已知函数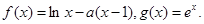
（1）求函数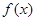的单调区间；
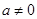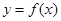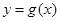（2）当时，过原点分别作曲线和的切线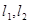，已知两切线的斜率互为倒数，证明：；
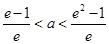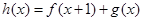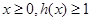（3）设，当时，求实数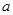的取值范围．

已知函数（）.
⑴ 若函数的图象在点处的切线的倾斜角为，求在上的最小值；
⑵ 若存在，使，求的取值范围．

已知函数的图像为曲线C，若曲线C存在与直线垂直的切线则实数m的取值范围是 （    ）

A．

B．

C．

D．

设函数（）．
（Ⅰ）若曲线过点，求曲线在点处的切线方程；
（Ⅱ）求函数在区间上的最大值．

已知．
（1）若，求曲线在点处的切线方程；
（2）若求函数的单调区间．

（本小题满分16分）已知函数，，.
（1）若曲线与直线相切，求实数的值；
（2）记，求在上的最大值；
（3）当时，试比较与的大小.

已知函数f（x）=k（x﹣1）e^x+x²．
（Ⅰ）当时k=﹣，求函数f（x）在点（1，1）处的切线方程；
（Ⅱ）若在y轴的左侧，函数g（x）=x²+（k+2）^x的图象恒在f（x）的导函数f′（x）图象的上方，求k的取值范围；
（Ⅲ）当k≤﹣l时，求函数f（x）在[k，1]上的最小值m．

设函数．
（1）若函数在处有极值，求函数的最大值；
（2）是否存在实数，使得关于的不等式在上恒成立？若存在，求出的取值范围；若不存在，说明理由；
（3）证明：不等式．