高中数学选择题

已知实数满足约束条件，则的最大值为（    ）．

A．24

B．20

C．16

D．12

已知，则=（   ）

A．

B．

C．

D．

由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数（史称戴德金分割）,并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集划分为两个非空的子集与,且满足,,中的每一个元素都小于中的每一个元素,则称为戴德金分割.试判断,对于任一戴德金分割,下列选项中,不可能成立的是（   ）

A．没有最大元素,有一个最小元素

B．没有最大元素,也没有最小元素

C．有一个最大元素,有一个最小元素

D．有一个最大元素,没有最小元素

已知在上是奇函数,且满足,当时,,则（ ）

A．

B．

C．

D．

已知全集U={1，2，3，4，5，6}，集合M={1，3，5}，则

A．

B．{1，3，5}

C．{2，4，6}

D．{1，2，3，4，5，6}

若某几何体的三视图如图所示，则这个几何体的体积是（ ）

A．5

B．6

C．7

D．8

函数的图像恒过定点，若点在直线上，则的最小值为（  ）

A．

B．

C．

D．

某同学在研究函数 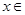（R）时，分别给出下面几个结论：
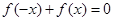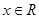①等式在时恒成立； 
②函数 f（x）的值域为 （－1,1）；
③若x₁≠x₂，则一定有f （x₁）≠f （x₂）；
④函数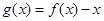在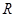上有三个零点．
其中正确结论的序号是（   ）

A．①②

B．①②③

C．①③④

D．①②③④

已知函数f（x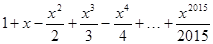）＝，则下列结论正确的是

A．f（x）在（0,1）上恰有一个零点

B．f（x）在（－1,0）上恰有一个零点

C．f（x）在（0,1）上恰有两个零点

D．f（x）在（－1,0）上恰有两个零点

如图，正方体ABCD—A₁B₁C₁D₁中，O为底面ABCD的中心，
M为棱BB₁的中点，则下列结论中错误的是（  ）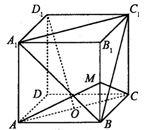

A．D1O∥平面A1BC1

B．D1O⊥平面AMC

C．异面直线BC1与AC所成的角等于60°

D．二面角M－AC－B等于45°

若函数为定义在上的奇函数，且在为增函数，又，则不等式的解集为（        ）

A．

B．

C．

D．

三个数的大小关系为（        ）

A．

B．

C．

D．

在下列区间中，函数的零点所在的区间为（    ）

A．

B．

C．

D．

已知是椭圆长轴的两个端点， 是椭圆上关于轴对称的两点，直线的斜率分别为，若椭圆的离心率为,则的最小值为（    ）

A．

B．

C．

D．

若椭圆与双曲线有相同的焦点F₁、F₂，P是这两条曲线的一
个交点，则的面积是（   ）

A．4

B．2

C．1

D．