(本小题满分12分)某班同学利用国庆节进行社会实践,对 [25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图: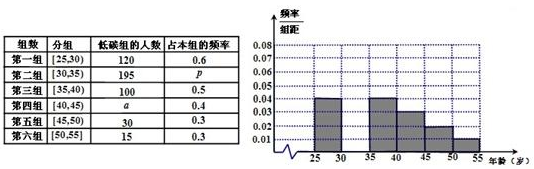
(1)补全频率分布直方图并求n、a、p的值;
(2)从[40,50)岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁的人数为X,求X的分布列和期望E(X).
已知函数f(x)是定义在R上的增函数.
(1)a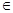 R,试比较f(a2)与f(a-1)的大小,并说明理由;
R,试比较f(a2)与f(a-1)的大小,并说明理由;
(2)若对任意的x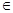 R,不等式f(ax2)﹤f(ax+1)恒成立.求实数a的取值范围.
R,不等式f(ax2)﹤f(ax+1)恒成立.求实数a的取值范围.
(本小题满分12分)据报道,某公司的33名职工的月工资(以元为单位)如下:
| 职务 |
董事长 |
副董事长 |
董事 |
总经理 |
经理 |
管理员 |
职员 |
| 人数 |
1 |
1 |
2 |
1 |
5 |
3 |
20 |
| 工资 |
5 500 |
5 000 |
3 500 |
3 000 |
2 500 |
2 000 |
1 500 |
(1)求该公司职工月工资的平均数、中位数、众数;
(2)假设副董事长的工资从5 000元提升到20 000元,董事长的工资从5 500元提升到30 000元,那么新的平均数、中位数、众数又是什么?(精确到元)
(3)你认为哪个统计量更能反映这个公司员工的工资水平?结合此问题谈一谈你的看法.
(本小题满分12分)已知二次函数f(x)满足:函数f(x+1)为偶函数,f(x)的最小值为-4,函数f(x)的图象与x轴交点为A、B,且AB=4,求二次函数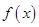 的解析式.
的解析式.
在△ABC中,角A,B,C的对应边分别是a,b,c满足b2+c2=bc+a2.
(Ⅰ)求角A的大小;
(Ⅱ)已知等差数列{an}的公差不为零,若a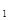 cosA=1,且a 2 ,a 4 ,a 8成等比数列,求{
cosA=1,且a 2 ,a 4 ,a 8成等比数列,求{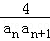 }的前n项和Sn.
}的前n项和Sn.
如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
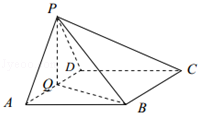
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,且PM=3MC,求三棱锥P﹣QBM的体积.
试题篮
()