一条直线经过点P(3,2),并且分别满足下列条件,求直线方程:
(1)倾斜角是直线x-4y+3=0的倾斜角的2倍;
(2)与x、y轴的正半轴交于A、B两点,且△AOB的面积最小(O为坐标原点).
(本小题满分12分)已知二次函数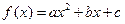
 为实数a不为零
为实数a不为零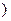 ,且同时满足下列条件:
,且同时满足下列条件:  ;
;
(2)对于任意的实数x,都有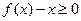 ;
; (3)当
(3)当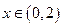 时有
时有 。
。
(1)求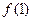 ; (2)求
; (2)求 的值;
的值;
(3)当 时,函数
时,函数 是单调函数,求
是单调函数,求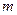 的取值范围。
的取值范围。
(本小题满分12分)已知函数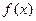 的定义域为(0,+∞),且满足对任意的
的定义域为(0,+∞),且满足对任意的 >0,y>0,
>0,y>0,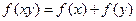 ,
,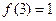 .当
.当 >1时,
>1时,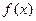 >0.
>0.
(1)求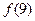 的值
的值
(2)判断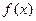 的单调性,并加以证明
的单调性,并加以证明
(3)解不等式 .
.
试题篮
()