高中数学解答题

（本小题满分13分）
已知函数为自然对数的底数）
（1）求的单调区间，若有最值，请求出最值；
（2）是否存在正常数，使的图象有且只有一个公共点，且在该公共点处有共同的切线？若存在，求出的值，以及公共点坐标和公切线方程；若不存在，请说明理由。

已知椭圆E的中心在坐标原点，焦点在x轴上，离心率为，且椭圆E上一点到两个焦点距离之和为4；是过点P（0，2）且互相垂直的两条直线，交E于A，B两点，交E交C，D两点，AB，CD的中点分别为M，N。
（1）求椭圆E的方程；
（2）求k的取值范围；
（3）求的取值范围。

（本小题满分13分）
在数列。
（1）求证：数列是等差数列，并求数列的通项公式；
（2）设，求数列的前项和。

在如图所示的空间几何体中，平面平面ABC，AB=BC=CA=DA=DC=BE=2，BE和平面ABC所成的角为60°，且点E在平面ABC上的射影落在的平分线上。
（1）求证：DE//平面ABC；
（2）求二面角E—BC—A的余弦；
（3）求多面体ABCDE的体积。

甲乙两个盒子里各放有标号为1，2，3，4的四个大小形状完全相同的小球，从甲盒中任取一小球，记下号码后放入乙盒，再从乙盒中任取一小球，记下号码，设随机变量
（1）求的概率；
（2）求随机变量X的分布列及数学期望。

（本小题满分12分）
在，角A，B，C的对边分别为。
（1）判断的形状；
（2）若的值。

(满分12分)已知为偶函数，曲线过点，且.
(Ⅰ)若曲线有斜率为0的切线，求实数的取值范围
(Ⅱ)若当时函数取得极大值，且方程有三个不同的实数解，求实数的取值范围.

(满分12分)函数的定义域为，且满足对于任意的实数，有.
(Ⅰ)求的值；       (Ⅱ)判断的奇偶性并证明；
（III）若，且在上是增函数，解关于的不等式.

(满分12分) 已知函数.
(Ⅰ)求函数的反函数解析式;
(Ⅱ)判断函数的奇偶性;
（III）当时,解不定式.

(满分12分)设函数，其中常数a>1.
(Ⅰ)讨论f(x)的单调性；
(Ⅱ)若当x≥0时，f(x)>0恒成立，求a的取值范围.

某高级中学共有学生2000名，各年级男、女生人数如下表：

	高一年级	高二年级	高三年级
女生	373	x	y
男生	377	370	z

已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.19.
(Ⅰ)求x的值；
(Ⅱ)现用分层抽样的方法在全校抽取48名学生，问应在高三年级抽取多少名？

(满分12分)设命题P:关于x的不等式的解集为;命题Q：的定义域为R.如果P或Q为真,P且Q为假,求的取值范围.

本题有（1）、（2）、（3）三个选考题，每题7份，请考生任选2题作答，满分14分.
如果多做，则按所做的前两题计分.
选修4系列（本小题满分14分）
（1）（本小题满分7分）选修4-2：矩阵与变换
设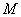是把坐标平面上的点的横坐标伸长到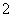倍，纵坐标伸长到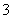倍的伸压变换．
（Ⅰ）求矩阵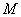的特征值及相应的特征向量；
（Ⅱ）求逆矩阵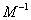以及椭圆在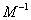的作用下的新曲线的方程．
(2)（本小题满分7分）选修4-4：坐标系与参数方程
直角坐标系中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，已知直线l的极坐标方程，曲线C的参数方程为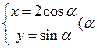为参数），求曲线C截直线l所得的弦长
（3）（本小题满分7分）选修4—5：不等式选讲
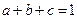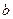已知，且、、是正数，求证：.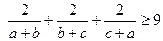

（本小题满分14分）
已知函数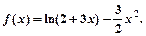
（1）求f(x)在[0，1]上的极值；
（2）若对任意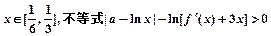成立，求实数a的取值范围；
（3）若关于x的方程在[0，2]上恰有两个不同的实根,求实数b的取值范围.

（本小题满分13分）

过椭圆内一点M(1，1)的弦AB
(1）若点M恰为弦AB的中点，求直线AB的方程；   
（2）求过点M的弦的中点的轨迹方程。