已知椭圆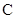 的中心为坐标原点,其离心率为
的中心为坐标原点,其离心率为 ,椭圆
,椭圆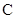 的一个焦点和抛物线
的一个焦点和抛物线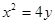 的焦点重合。
的焦点重合。
(1)求椭圆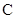 的方程
的方程
(2)过点 的动直线
的动直线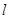 交椭圆
交椭圆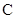 于
于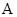 、
、 两点,试问:在坐标平面上是否存
两点,试问:在坐标平面上是否存在一个定点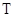 ,使得无论
,使得无论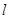 如何转动,以
如何转动,以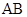 为直径的圆恒过点
为直径的圆恒过点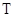 ,若存在,说出点
,若存在,说出点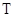 的坐标,若不存在,说明理由。
的坐标,若不存在,说明理由。
如图,A,B是双曲线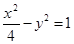 的左.右顶点,C,D是双曲线上关于x轴对称的两点,直线AC与BD的交点为E.
的左.右顶点,C,D是双曲线上关于x轴对称的两点,直线AC与BD的交点为E.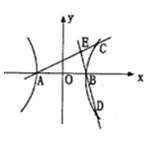
(1)求点E的轨迹W的方程;
(2)若W与x轴的正半轴,y轴的正半轴的交点分别为M,N,直线y=kx(k>0)与W的两个交点分别是P,Q(其中P是第一象限),求四边形MPNQ面积的最大值.
在直角坐标系 中,以
中,以 为极点,
为极点, 轴正半轴为极轴建立极坐标系.圆
轴正半轴为极轴建立极坐标系.圆 ,直线
,直线 的极坐标方程分别为
的极坐标方程分别为 .
.
(Ⅰ)求 与
与 交点的极坐标;
交点的极坐标;
(Ⅱ)设 为
为 的圆心,
的圆心, 为
为 与
与 交点连线的中点.已知直线
交点连线的中点.已知直线 的参数方程为
的参数方程为 (
( 为参数),求
为参数),求 的值.
的值.
已知函数 ,其中
,其中 .
.
(1)设函数 ,若当
,若当 时,
时, 有意义,求
有意义,求 的取值范围;
的取值范围;
(2)是否存在是实数 ,使得关于
,使得关于 的方程
的方程 对于任意非正实数
对于任意非正实数 ,均有实数根?若存在,求
,均有实数根?若存在,求 ;若不存在,说明理由.
;若不存在,说明理由.
试题篮
()