高中数学解答题

金融机构对本市内随机抽取的20家微小企业的产业结构调整及生产经营情况进行评估，根据得分将企业评定为优秀、良好、合格、不合格四个等级，金融机构将根据等级对企业提供相应额度的资金支持。

（1）在答题卡上作出频率分布直方图，并由此估计该市微小企业所获资金支持的均值；
（2）金融机构鼓励得分前2名的两家企业A、B随机收购得分后2名的两家企业a、b中的一家，求A、B企业选择收购同一家企业的概率。

如图，为了测量河对岸A、B两点之间的距离，观察者找到一个点C，从C点可以观察到点A、B；找到一个点D，从D点可以观察到点A、C：找到一个点E，从E点可以观察到点B、C。并测得以下数据：CD=CE=100m，∠ACD=90°，∠ACB=45°，∠BCE=75°，∠CDA=∠CEB=60°，求A、B两 点之间的距离。

已知函数f(x)=|x+1|+|x﹣2|﹣m
（I）当时，求f(x) >0的解集；
（II）若关于的不等式f(x) ≥2的解集是，求的取值范围

已知函数
（Ⅰ）当a=﹣2时，求函数f(x)的单调区间；
（Ⅱ）若g(x)= +在1，+∞)上是单调函数，求实数a的取值范围.

我校高三年级进行了一次水平测试.用系统抽样的方法抽取了50名学生的数学成绩,准备进行分析和研究.经统计成绩的分组及各组的频数如下:
[40,50), 2;   [50,60), 3;  [60,70), 10;  [70,80), 15;   [80,90), 12;  [90,100], 8.
（Ⅰ）完成样本的频率分布表；画出频率分布直方图.
（Ⅱ）估计成绩在85分以下的学生比例；
（Ⅲ）请你根据以上信息去估计样本的众数、中位数、平均数.（精确到0.01）
（Ⅰ）频率分布表

分组	频数	频率
[40,50)	2
[50,60)	3
[60,70)	10
[70,80)	15
[80,90)	12
[90,100]	8
合计	50

 
(Ⅰ)频率分布直方图为

已知公比大于1的等比数列{}满足：++=28，且+2是和的等差中项.
（Ⅰ）求数列{}的通项公式；
（Ⅱ）若=，求{}的前n项和.

设平面内两定点、，直线和相交于点,且它们的斜率之积为定值。
（I）求动点的轨迹的方程；
（II）设，过点作抛物线的切线交曲线于、两点，求的面积。

某项新技术进入试用阶段前必须对其中三项不同指标甲、乙、丙进行通过量化检测。假设该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为，指标甲、乙、丙检测合格分别记4分、2分、4分，若某项指标不合格，则该项指标记0分，各项指标检测结果互不影响。
（Ⅰ）求该项技术量化得分不低于8分的概率；
（Ⅱ）记该技术的三个指标中被检测合格的指标个数为随机变量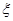，求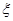的分布列与数学期望。

已知函数
（I）若，求sin2x的值；
（II）求函数的最大值与单调递增区间.

（本小题满分12分）已知的展开式中第4项与第8项的二项式系数相等.
（Ⅰ）求的值；
（Ⅱ）求第4项与第8项的系数之和.

（本小题满分10分）从名男生和名女生中选出人参加学校辩论赛.
（Ⅰ）如果人中男生和女生各选人，有多少种选法？
（Ⅱ）如果男生中的甲和女生中的乙至少有1人在内，有多少种选法？

已知．
⑴化简
⑵

设锐角三角形ABC的内角A、B、C的对边分别为a、b、c，a=2bsinA   （1）求B的大小；(2) 若a=3,c=5,求b.

如图所示一个空间几何体的正视图和俯视图都是边长为1的正方形，俯视图为圆，求这个几何体的下底面积和体积（可用公式：柱体体积=底面积×高，锥体体积=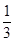×底面积×高）

求函数（）的最小值