高中数学解答题

学校从参加高二年级期中考试的学生中抽出50名学生，并统计了他们的数学成绩（成绩均为整数且满分为100分），数学成绩分组及各组频数如下：
[40，50），2；[50，60），3；[60，70），14；[70，80），15；[80，90），12；[90，100]，4．
（1）在给出的样本频率分布表中，求的值；
（2）估计成绩在80分以上（含80分）学生的比例；
（3）为了帮助成绩差的学生提高数学成绩，学校决定成立“二帮一”小组，即从成绩在[90，100]的学生中选两位同学，共同帮助成绩在[40，50）中的某一位同学．已知甲同学的成绩为42分，乙同学的成绩为95分，求甲、乙两同学恰好被安排在同一小组的概率．
样本频率分布表如下：

分组	频数	频率
[40，50）	2	0．04
[50，60）	3	0．06
[60，70）	14	0．28
[70，80）	15	0．30
[80，90）	A	B
[90，100]	4	0．08
合计	C	D

 

已知椭圆：的右焦点，过的直线交椭圆于两点，且是线段的中点．
（1）求椭圆的方程；
（2）已知是椭圆的左焦点，求的面积．

设函数
（Ⅰ）当，求函数的单调区间与极值；
（Ⅱ）若函数在上是增函数，求实数的取值范围．

选修；坐标系与参数方程
在直角坐标系中，直线的参数方程为（为参数），若以原点为极点，轴正半轴为极轴建立极坐标系，已知圆的极坐标方程为，设是圆上任一点，连结并延长到，使．
（Ⅰ）求点轨迹的直角坐标方程；
（Ⅱ）若直线与点轨迹相交于两点，点的直角坐标为，求的值．

甲、乙、丙三班进行知识竞赛，每两班比赛一场，共赛三场．每场比赛胜者得分，负者得分，没有平局，在每一场比赛中，甲班胜乙班的概率为，甲班胜丙班的概率为，乙班胜丙班的概率为．
（Ⅰ）求甲班获第一名且丙班获第二名的概率；
（Ⅱ）设在该次比赛中，甲班得分为，求的分布列和数学期望．

选修：几何证明选讲
如图，过点作圆的割线与切线，为切点，连接，的平分线与分别交于点，其中．

（Ⅰ）求证：；
（Ⅱ）求的大小．

已知椭圆的离心率为，以原点为圆心，椭圆的短半轴长为半径的圆与直线相切．是椭圆的右顶点与上顶点，直线与椭圆相交于两点．

（Ⅰ）求椭圆的方程；
（Ⅱ）当四边形面积取最大值时，求的值．

选修4-4:坐标系与参数方程
在直角坐标平面内，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，直线和曲线（为参数）．
（1）将与的方程化为普通方程；
（2）判定直线l与曲线 是否相交，若相交求出被截得的弦长．

在底面是矩形的四棱锥P­ABCD中，PA⊥平面ABCD，PA＝AB＝2，BC＝4，E是PD的中点．

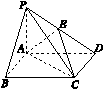
（1）求证：平面PDC⊥平面PAD；
（2）求二面角E­AC­D的余弦值；
（3）求直线CD与平面AEC所成角的正弦值．

如图所示，在长方体中，，，M是棱的中点.

（1）求异面直线和所成的角的正切值；
（2）证明：平面平面.

集合， .
（1）若，求实数m的取值范围；
（2）当时，求A的非空真子集的个数.

已知动圆过定点，且在轴上截得的弦长．
（Ⅰ）求动圆圆心的轨迹方程；
（Ⅱ）若过点的直线交圆心的轨迹于点，，且，求直线的方程．

已知函数．
（1）求函数的最小正周期和单调递增区间；
（2）当时,若恒成立,求的取值范围．

已知集合．
（1）当时，求；
（2）求使的实数的取值范围．

选修4-5：不等式选讲
设函数．
（1）若,解不等式；
（2）若函数有最小值，求实数的取值范围．