高中数学解答题

已知集合，集合，若满足，求实数a的取值范围．

已知函数f（x）对任意实数x，y，均有f（x＋y）＝f（x）＋f（y），且当x＞0时，f（x）＞0，f（－1）＝－2，求f（x）在区间[－2，1]上的值域．

已知f (x)是R上的偶函数，且在(0,+ )上单调递增，并且f (x)<0对一切成立，试判断在(－,0)上的单调性，并证明你的结论．

证明：函数f（x）＝在（－2，＋¥）上是增函数．

已知A=，B＝．
（Ⅰ）若，求的取值范围；
（Ⅱ）若，求的取值范围．

若，求实数的值。

设全集为R,已知，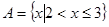
（1）若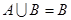，求实数的取值范围
（2）若，求实数的取值范围
（3）若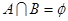，求实数的取值范围

已知集合，，
（1）求，；
（2），

已知函数，
（1）证明在（1，+∞）上是减函数；
（2）当时，求的最小值和最大值。

设全集为实数集R，，，．
（1）求及;
（2）如果，求a的取值范围．

（1）计算：
（2）计算：；

已知全集，其中，
（1）求  （2） 求

已知定义在的函数
（1）试判断的奇偶性。
（2）若函数在上为增函数，解关于的不等式。

某车间生产一种仪器的固定成本是10000元，每生产一台该仪器需要增加投入100元，已知总收入满足函数：，其中是仪器的月产量（总收入＝总成本＋利润）．
（Ⅰ）将利润（用表示）表示为月产量的函数；
（Ⅱ）当月产量为何值时，车间所获利润最大？最大利润是多少元？

已知抛物线，过点的直线交C于A，B两点，抛物线C在点A处的切线与在点B处的切线交于点P．

（1）若直线的斜率为1，求；
（2）求面积的最小值．