已知函数 .
(1)若 ,求a的值;
(2)设m为整数,且对于任意正整数n, ,求m的最小值.
已知抛物线C:y2=2x,过点(2,0)的直线l交C于A,B两点,圆M是以线段AB为直径的圆.
(1)证明:坐标原点O在圆M上;
(2)设圆M过点 ,求直线l与圆M的方程.
如图,四面体 ABCD中, 是正三角形, 是直角三角形, .
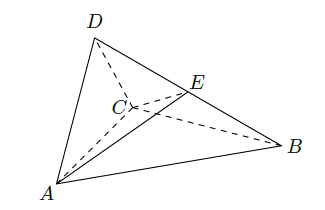
(1)证明: ;
(2)过 AC的平面交 BD于点 E,若平面 AEC把四面体 ABCD分成体积相等的两部分,求二面角 的余弦值.
某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 |
[10,15) |
[15,20) |
[20,25) |
[25,30) |
[30,35) |
[35,40) |
天数 |
2 |
16 |
36 |
25 |
7 |
4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
的内角  的对边分别为
已知
.
的对边分别为
已知
.
(1)求角 和边长 ;
(2)设
为
边上一点,且 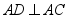 ,求
的面积.
,求
的面积.
已知抛物线C: =2px经过点 (1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(Ⅰ)求直线l的斜率的取值范围;
(Ⅱ)设O为原点, , ,求证: 为定值.
设函数 =[ ] .
(1)若曲线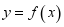 在点(1,
)处的切线与
轴平行,求
;
在点(1,
)处的切线与
轴平行,求
;
(2)若 在 处取得极小值,求 的取值范围.
电影公司随机收集了电影的有关数据,经分类整理得到下表:
| 电影类型 |
第一类 |
第二类 |
第三类 |
第四类 |
第五类 |
第六类 |
| 电影部数 |
140 |
50 |
300 |
200 |
800 |
510 |
| 好评率 |
0.4 |
0.2 |
0.15 |
0.25 |
0.2 |
0.1 |
好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.
假设所有电影是否获得好评相互独立.
(Ⅰ)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;
(Ⅱ)从第四类电影和第五类电影中各随机选取1部,估计恰有1部获得好评的概率;
(Ⅲ)假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等,用" "表示第 k类电影得到人们喜欢," "表示第 k类电影没有得到人们喜欢( k=1,2,3,4,5,6).写出方差 , , , , , 的大小关系.
如图,在三棱柱 ABC−
中,
平面 ABC, D, E, F, G分别为
, AC,
,  的中点, AB=BC=
, AC=
=2.
的中点, AB=BC=
, AC=
=2.
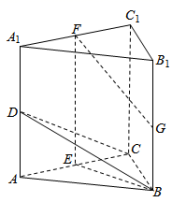
(1)求证: AC⊥平面 BEF;
(2)求二面角 B−CD− C 1的余弦值;
(3)证明:直线 FG与平面 BCD相交.
设椭圆 (a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为 ,点A的坐标为 ,且 .
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线l: 与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若 (O为原点) ,求k的值.
设 是等比数列,公比大于0,其前n项和为 , 是等差数列.已知 , , , .
(I)求 和 的通项公式;
(II)设数列 的前n项和为 ,
(i)求 ;
(ii)证明 .
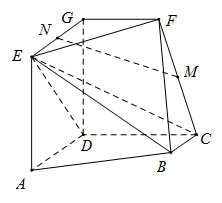
如图, 且AD=2BC, , 且EG=AD, 且CD=2FG, ,DA=DC=DG=2.
(Ⅰ)若M为CF的中点,N为EG的中点,求证: ;
(Ⅱ)求二面角 的正弦值;
(Ⅲ)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.
已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(I)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;
(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
试题篮
()