一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
如图所示,设铁路AB=50,B、C之间距离为10,现将货物从A运往C,已知单位距离铁路费用为2,公路费用为4,问在AB上何处修筑公路至C,可使运费由A到C最省?
某种产品每件成本为6元,每件售价为x元(x>6),年销量为u万件,若已知 与
与 成正比,且售价为10元时,年销量为28万件.
成正比,且售价为10元时,年销量为28万件.
(1)求年销售利润y关于x的函数关系式.
(2)求售价为多少时,年利润最大,并求出最大年利润.
用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少?
已知:函数f(x)=x3﹣6x+5,x∈R,
(1)求:函数f(x)的单调区间和极值;
(2)若关于x的方程f(x)=a有3个不同实根,求:实数a的取值范围;
(3)当x∈(1,+∞)时,f(x)≥k(x﹣1)恒成立,求:实数k的取值范围.
设函数f(x)=﹣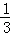 x3+2ax2﹣3a2x+b,0<a<1.
x3+2ax2﹣3a2x+b,0<a<1.
(1)求函数f(x)的单调区间、极值;
(2)若x∈[0,3a],试求函数f(x)的最值.
已知函数f(x)=﹣x3+3x2+9x+a.
(Ⅰ)求f(x)的单调递减区间;
(Ⅱ)若f(x)在区间[﹣2,2]上的最大值为20,求它在该区间上的最小值.
已知函数f(x)=x3﹣3x.
(1)求函数f(x)在[﹣3, ]上的最大值和最小值;
]上的最大值和最小值;
(2)过点P(2,﹣6)作曲线y=f(x)的切线,求此切线的方程.
试题篮
()