高中数学解答题

设f（x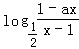）=为奇函数，a为常数．
（1）求a的值；并判断f（x）在区间（1，+∞）上的单调性；
（2）若对于区间（3，4）上的每一个x的值，不等式f（x）＞恒成立，求实数m的取值范围．

通过研究学生的学习行为，心理学家发现，学生的接受能力依赖于教师引入概念和描述问题所用的时间．讲座开始时，学生的兴趣激增；中间有一段不太长的时间，学生的兴趣保持较理想的状态，随后学生的注意力开始分散．分析结果和实验表明，用f（x）表示学生的接受能力，x表示引入概念和描述问题所用的时间（单位：分钟），可有以下的公式：
f（x）=
（1）开讲后多少分钟，学生的接受能力最强？能维持多长时间？
（2）一道数学难题，需要55的接受能力以及13分钟，教师能否及时在学生一直达到所需接受能力的状态下讲授完这道难题？

已知某几何体的俯视图是如图所示的矩形，正视图（或称主视图）是一个底边长为8、高为3的等腰三角形，侧视图（或称左视图）是一个底边长为6、高为3的等腰三角形．

（1）求该几何体的体积V；
（2）求该几何体的侧面积S．

定义在D上的函数f（x），如果满足对任意x∈D，存在常数M＞0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的上界，已知函数f（x）=1+x+ax²
（1）当a=﹣1时，求函数f（x）在（﹣∞，0）上的值域，判断函数f（x）在（﹣∞，0）上是否为有界函数，并说明理由；
（2）若函数f（x）在x∈[1，4]上是以3为上界的有界函数，求实数a的取值范围．

电信局为了配合客户不同需要，设有A，B两种优惠方案．这两种方案应付话费（元）与通话时间x（min）之间的关系如图所示，其中D的坐标为（，230）．

（1）若通话时间为2小时，按方案A，B各付话费多少元？
（2）方案B从500分钟以后，每分钟收费多少元？
（3）通话时间在什么范围内，方案B比方案A优惠？

已知函数f（x）是定义域在R上的奇函数，当x＞0时，f（x）=x²﹣2x．
（1）求出函数f（x）在R上的解析式；
（2）写出函数的单调区间．

已知向量=（cosα，sinα），=（cosβ，sinβ），|﹣|=．
（1）求cos（α﹣β）的值；
（2）若0＜α＜，﹣＜β＜0，且sinβ=﹣，求sinα．

在三角形ABC中，ABC表示三角形ABC的三个内角．sinA=（1+cosA）
（1）求：角A
（2）若．求：角B．

已知向量=（1，2），=（2，2）．
（1）求（2﹣）•（2+）；
（2）设=（﹣3，λ），若与夹角为钝角，求λ的值．

已知函数f（x）=2sinxcosx﹣2sin²x+1．
（1）x∈[0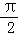，]，求函数f（x）的值域；
（2）x∈[0，π]，求f（x）的单调递增区间．

已知向量与的夹角为60°，||=1，||=2
（1）求（2﹣）•；
（2）求：|2+|．

已知函数f（x）=log₂+log₂（x﹣1）+log₂（p﹣x）．
（1）求函数f（x）的定义域；
（2）求函数f（x）的值域．

已知函数（x∈[1，+∞）且m＜1）．
（Ⅰ）用定义证明函数f（x）在[1，+∞）上为增函数；
（Ⅱ）设函数，若[2，5]是g（x）的一个单调区间，且在该区间上g（x）＞0恒成立，求实数m的取值范围．

某工厂对某种产品的产量与成本的资料分析后有如下数据：

产量x（千件）	2	3	5	6
成本y（万元）	7	8	9	12

 
经过分析，知道产量x和成本y之间具有线性相关关系．
（Ⅰ）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程；
（Ⅱ）试根据（1）求出的线性回归方程，预测产量为10千件时的成本．

已知椭圆C：的焦距为4，且与椭圆有相同的离心率，斜率为的直线经过点M（0，1），与椭圆C交于不同的两点A ，B．
（1）求椭圆C的标准方程；
（2）当椭圆C的右焦点F在以AB为直径的圆内时，求的取值范围．